题目内容
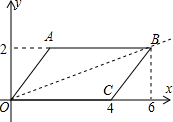
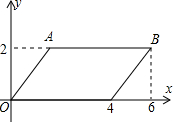 如图,在?OABC中,O(0,0),A(2,2),C(4,0),写出一个能将该平行四边形分成面积相等的两部分的直线的解析式:________.
如图,在?OABC中,O(0,0),A(2,2),C(4,0),写出一个能将该平行四边形分成面积相等的两部分的直线的解析式:________.
此题答案不唯一,如y=-x+4或y= x等.
x等.
分析:根据平行四边形的性质,可得过其对角线的交点的直线可将该平行四边形分成面积相等的两部分;比较简单的是连接OB或AC,利用待定系数法即可求得直线AC与OB的解析式.
解答: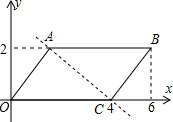 解:①连接AC,
解:①连接AC,
∵四边形OABC是平行四边形,
∴OA=BC,OA∥BC,
∴S△OAC=S△ABC,
设直线AC的解析式为:y=kx+b,
∵A(2,2),C(4,0),
∴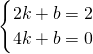 ,
,
解得: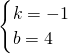 ,
,
∴直线AC的解析式为:y=-x+4;
 ②连接OB,
②连接OB,
同理:S△AOB=S△BOC,
∵在?OABC中,O(0,0),A(2,2),C(4,0),
∴B(6,2),
设直线OB的解析式为:y=mx,
∴6m=2,
解得:m= ,
,
∴直线OB的解析式为:y= x.
x.
故答案为:此题答案不唯一,如y=-x+4或y= x等.
x等.
点评:此题考查了平行线的性质以及待定系数法求一次解析式.此题难度适中,此题属于开放题,注意掌握方程思想与数形结合思想的应用.
 x等.
x等.分析:根据平行四边形的性质,可得过其对角线的交点的直线可将该平行四边形分成面积相等的两部分;比较简单的是连接OB或AC,利用待定系数法即可求得直线AC与OB的解析式.
解答:
 解:①连接AC,
解:①连接AC,∵四边形OABC是平行四边形,
∴OA=BC,OA∥BC,
∴S△OAC=S△ABC,
设直线AC的解析式为:y=kx+b,
∵A(2,2),C(4,0),
∴
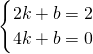 ,
,解得:
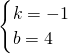 ,
,∴直线AC的解析式为:y=-x+4;
 ②连接OB,
②连接OB,同理:S△AOB=S△BOC,
∵在?OABC中,O(0,0),A(2,2),C(4,0),
∴B(6,2),
设直线OB的解析式为:y=mx,
∴6m=2,
解得:m=
 ,
,∴直线OB的解析式为:y=
 x.
x.故答案为:此题答案不唯一,如y=-x+4或y=
 x等.
x等.点评:此题考查了平行线的性质以及待定系数法求一次解析式.此题难度适中,此题属于开放题,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
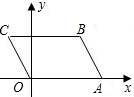 如图,在OABC中OA=a,AB=b,∠AOC=120°,则点C、B的坐标分别为
如图,在OABC中OA=a,AB=b,∠AOC=120°,则点C、B的坐标分别为 (2012•漳州)如图,在?OABC中,点A在x轴上,∠AOC=60°,0C=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
(2012•漳州)如图,在?OABC中,点A在x轴上,∠AOC=60°,0C=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒. 如图,在?OABC中,O(0,0),A(2,2),C(4,0),写出一个能将该平行四边形分成面积相等的两部分的直线的解析式:
如图,在?OABC中,O(0,0),A(2,2),C(4,0),写出一个能将该平行四边形分成面积相等的两部分的直线的解析式: OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
 OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.