题目内容
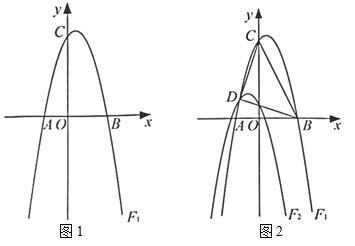
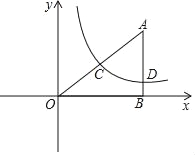
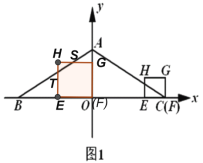
【题目】如图1,平面直角坐标系![]() 中,等腰
中,等腰![]() 的底边
的底边![]() 在
在![]() 轴上,
轴上,![]() ,顶点
,顶点![]() 在
在![]() 的正半轴上,
的正半轴上,![]() ,一动点
,一动点![]() 从
从![]() 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿![]() 向左运动,到达
向左运动,到达![]() 的中点停止.另一动点
的中点停止.另一动点![]() 从点
从点![]() 出发,以相同的速度沿
出发,以相同的速度沿![]() 向左运动,到达点
向左运动,到达点![]() 停止.已知点
停止.已知点![]() 、
、![]() 同时出发,以
同时出发,以![]() 为边作正方形
为边作正方形![]() ,使正方形
,使正方形![]() 和
和![]() 在
在![]() 的同侧.设运动的时间为
的同侧.设运动的时间为![]() 秒(
秒(![]() ).
).
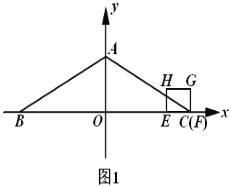
(1)当点![]() 落在
落在![]() 边上时,求
边上时,求![]() 的值;
的值;
(2)设正方形![]() 与
与![]() 重叠面积为
重叠面积为![]() ,请问是存在
,请问是存在![]() 值,使得
值,使得![]() ?若存在,求出
?若存在,求出![]() 值;若不存在,请说明理由;
值;若不存在,请说明理由;
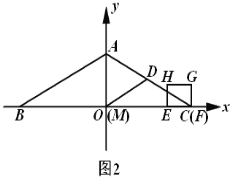
(3)如图2,取![]() 的中点
的中点![]() ,连结
,连结![]() ,当点
,当点![]() 、
、![]() 开始运动时,点
开始运动时,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 运动,到达点
运动,到达点![]() 停止运动.请问在点
停止运动.请问在点![]() 的整个运动过程中,点
的整个运动过程中,点![]() 可能在正方形
可能在正方形![]() 内(含边界)吗?如果可能,求出点
内(含边界)吗?如果可能,求出点![]() 在正方形
在正方形![]() 内(含边界)的时长;若不可能,请说明理由.
内(含边界)的时长;若不可能,请说明理由.
【答案】(1)t=1;(2)存在,![]() ,理由见解析;(3)可能,
,理由见解析;(3)可能,![]() 或
或![]() 或
或![]() 理由见解析
理由见解析
【解析】
(1)用待定系数法求出直线AC的解析式,根据题意用t表示出点H的坐标,代入求解即可;
(2)根据已知,当点F运动到点O停止运动前,重叠最大面积是边长为1的正方形的面积,即不存在t,使重叠面积为![]() ,故t﹥4,用待定系数法求出直线AB的解析式,求出点H落在BC边上时的t值,求出此时重叠面积为
,故t﹥4,用待定系数法求出直线AB的解析式,求出点H落在BC边上时的t值,求出此时重叠面积为![]() ﹤
﹤![]() ,进一步求出重叠面积关于t的表达式,代入解t的方程即可解得t值;
,进一步求出重叠面积关于t的表达式,代入解t的方程即可解得t值;
(3)由已知求得点D(2,1),AC=![]() ,OD=OC=OA=
,OD=OC=OA=![]() ,结合图形分情况讨论即可得出符合条件的时长.
,结合图形分情况讨论即可得出符合条件的时长.
(1)由题意,A(0,2),B(-4,0),C(4,0),
设直线AC的函数解析式为y=kx+b,
将点A、C坐标代入,得:
![]() ,解得:
,解得: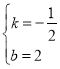 ,
,
∴直线AC的函数解析式为![]() ,
,
当点![]() 落在
落在![]() 边上时,点E(3-t,0),点H(3-t,1),
边上时,点E(3-t,0),点H(3-t,1),
将点H代入![]() ,得:
,得:
![]() ,解得:t=1;
,解得:t=1;
(2)存在,![]() ,使得
,使得![]() .
.
根据已知,当点F运动到点O停止运动前,重叠最大面积是边长为1的正方形的面积,即不存在t,使重叠面积为![]() ,故t﹥4,
,故t﹥4,
设直线AB的函数解析式为y=mx+n,
将点A、B坐标代入,得:
![]() ,解得:
,解得: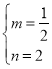 ,
,
∴直线AC的函数解析式为![]() ,
,
当t﹥4时,点E(3-t,0)点H(3-t,t-3),G(0,t-3),
当点H落在AB边上时,将点H代入![]() ,得:
,得:
![]() ,解得:
,解得:![]() ;
;
此时重叠的面积为![]() ,
,
∵![]() ﹤
﹤![]() ,∴
,∴![]() ﹤t﹤5,
﹤t﹤5,
如图1,设GH交AB于S,EH交AB于T,
将y=t-3代入![]() 得:
得:![]() ,
,
解得:x=2t-10,
∴点S(2t-10,t-3),
将x=3-t代入![]() 得:
得:![]() ,
,
∴点T![]() ,
,
∴AG=5-t,SG=10-2t,BE=7-t,ET=![]() ,
,
![]() ,
,
![]()
所以重叠面积S=![]() =4-
=4-![]() -
-![]() =
=![]() ,
,
由![]() =
=![]() 得:
得:![]() ,
,![]() ﹥5(舍去),
﹥5(舍去),
∴![]() ;
;
(3)可能,![]() ≤t≤1或t=4.
≤t≤1或t=4.
∵点D为AC的中点,且OA=2,OC=4,
∴点D(2,1),AC=![]() ,OD=OC=OA=
,OD=OC=OA=![]() ,
,
易知M点在水平方向以每秒是4个单位的速度运动;
当0﹤t﹤![]() 时,M在线段OD上,H未到达D点,所以M与正方形不相遇;
时,M在线段OD上,H未到达D点,所以M与正方形不相遇;
当![]() ﹤t﹤1时,
﹤t﹤1时, ![]() +
+![]() ÷(1+4)=
÷(1+4)=![]() 秒,
秒,
∴![]()
![]() 时M与正方形相遇,经过1÷(1+4)=
时M与正方形相遇,经过1÷(1+4)=![]() 秒后,M点不在正方行内部,则
秒后,M点不在正方行内部,则![]() ;
;
当t=1时,由(1)知,点F运动到原E点处,M点到达C处;
当1≤t≤2时,当t=1+1÷(4-1)=![]() 秒时,点M追上G点,经过1÷(4-1)=
秒时,点M追上G点,经过1÷(4-1)=![]() 秒,点
秒,点![]() 都在正方形
都在正方形![]() 内(含边界),
内(含边界),![]()
当t=2时,点M运动返回到点O处停止运动,
当 t=3时,点E运动返回到点O处, 当 t=4时,点F运动返回到点O处,
当![]() 时,点
时,点![]() 都在正方形
都在正方形![]() 内(含边界),
内(含边界),
综上,当![]() 或
或![]() 或
或![]() 时,点
时,点![]() 可能在正方形
可能在正方形![]() 内(含边界).
内(含边界).

【题目】为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看![]() 次的人数没有标出).
次的人数没有标出).
根据上述信息,解答下列各题:
 ×
×
(1)该班级女生人数是__________,女生收看“两会”新闻次数的中位数是________;
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于![]() 次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低![]() ,试求该班级男生人数;
,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 | 平均数(次) | 中位数(次) | 众数(次) | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.