��Ŀ����
����Ŀ���������֣�
![]() ��ͼ1����ֱ�����ǰ��ֱ�Ƕ������������ABCD�ϣ�ʹֱ�Ƕ���E��������ABCD�Ķ���D�غϣ�ֱ�ǵ�һ�߽�CB�ڵ�F������һ�߽�BA���ӳ����ڵ�
��ͼ1����ֱ�����ǰ��ֱ�Ƕ������������ABCD�ϣ�ʹֱ�Ƕ���E��������ABCD�Ķ���D�غϣ�ֱ�ǵ�һ�߽�CB�ڵ�F������һ�߽�BA���ӳ����ڵ�![]() ����ֱ�ӻش�EF��EG��������ϵ��
����ֱ�ӻش�EF��EG��������ϵ��
���̽��
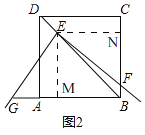
![]() ��ͼ2�������ǰ��ֱ�Ƕ���E��������ABCD�ĶԽ���BD���˶�ʱ�������������䣬
��ͼ2�������ǰ��ֱ�Ƕ���E��������ABCD�ĶԽ���BD���˶�ʱ�������������䣬![]() �еĽ��ۻ������𣿲�˵�����ɣ�
�еĽ��ۻ������𣿲�˵�����ɣ�
��չ����
![]() ��ͼ3������������ABCD���ij�������ABCD������ֱ�Ƕ����ƶ���ͼ����ʾλ��ʱ����
��ͼ3������������ABCD���ij�������ABCD������ֱ�Ƕ����ƶ���ͼ����ʾλ��ʱ����![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��

���𰸡���1��![]() ����2�����۳��������ɼ���������3��
����2�����۳��������ɼ���������3��![]() ��
��
��������
��1�����жϳ�CDF=��ADG�������жϳ���CDF�ա�ADG�����ɵó�DF=DG���۵�֤��
��2���ȹ����ͼ�Σ��жϳ���NEF=��MEG�������жϳ���NEF�ա�MEG�����ɵó�EF=EG��
��3�����жϳ���NEF=��MEG�������жϳ���ENF�ס�EMG���ó� ![]() ����֤��
����֤��![]() ���ɽ�����⣻���ɵó����ۣ�
���ɽ�����⣻���ɵó����ۣ�
![]() ֤����
֤����![]() �ı���ABCD�������Σ�
�ı���ABCD�������Σ�
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
��![]() ��
��![]() ��
�У�
 ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��D��E�غϣ�
��D��E�غϣ�
![]() ��
��
![]() �⣺���۳�����
�⣺���۳�����
���ɣ���ͼ2��
����E��![]() ��N��
��N��![]() ��M��
��M��
![]() ��E��������ABCD�ĶԽ���BD�ϣ�
��E��������ABCD�ĶԽ���BD�ϣ�
![]() �ı���EMBN�������Σ�
�ı���EMBN�������Σ�
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
��![]() ��
��![]() ��
�У�
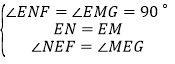 ��
��
![]() ��
��![]() ��
��
![]() ��
��
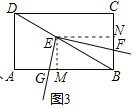
![]() �⣺��ͼ3������E��
�⣺��ͼ3������E��![]() ��N��
��N��![]() ��M��
��M��
![]() �ı���EMBN�Ǿ��Σ�
�ı���EMBN�Ǿ��Σ�
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��

����Ŀ�����¹���x�ĸ�������ʽ��,a,b,c,m,n��Ϊ����.
(1)���ݼ�������д�±���
������ϵ�� | һ����ϵ�� | ������ | |
(2x + l)(x + 2) | 2 | 2 | |
(2x + 1)(3x - 2) | 6 | -2 | |
(ax + b)( mx + n) | am | bn |
(2)��֪(x+ 3)2(x + mx +n)�Ȳ��������Ҳ����һ�����m + n��ֵ.
(3) ����ʽM�����ʽx2-3x + 1�ij˻�Ϊ2x4+ ax3 + bx2+ cx -3,��2 a +b + c��ֵΪ



