题目内容
已知△BCD中,BC=BD,以BD为直径⊙O的交BC于E,交CD于M.

(1)如图1,求证:
=
.
(2)如图2,过B作BA∥CD交⊙O于A,若CE=2,CM=
,求AE的长.

(1)如图1,求证:
 |
| DM |
 |
| EM |
(2)如图2,过B作BA∥CD交⊙O于A,若CE=2,CM=
| 6 |
(1)连接BM,如图1所示,
∵BD为圆O的直径,
∴∠BMD=90°,即BM⊥CD,
∵BD=BC,
∴BM平分∠DBC,即∠DBM=∠CBM,
∴
=
;
(2)连接AD,EM,DE,如图2所示,
∵BD为圆O的直径,
∴∠DEC=90°,
在Rt△DEC中,CE=2,DC=2CM=2
,
根据勾股定理得:DE=
=2
,
∵∠DEC=∠BMC=90°,∠C=∠C,
∵△DEC∽△BMC,
∴
=
,即BM=
=
,
∵AB∥DC,
∴∠BAD=∠ADM=90°,
∵∠BMD=90°,
∴四边形ABMD为矩形,
∴AB=DM,
∴
=
,
∵
=
,
∴
=
,
∴
+
=
+
,即
=
,
∴AE=BM=
.
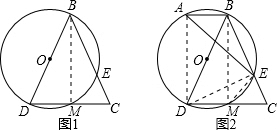
∵BD为圆O的直径,
∴∠BMD=90°,即BM⊥CD,
∵BD=BC,
∴BM平分∠DBC,即∠DBM=∠CBM,
∴
 |
| DM |
 |
| EM |
(2)连接AD,EM,DE,如图2所示,
∵BD为圆O的直径,
∴∠DEC=90°,
在Rt△DEC中,CE=2,DC=2CM=2
| 6 |
根据勾股定理得:DE=
| DC2-CE2 |
| 5 |
∵∠DEC=∠BMC=90°,∠C=∠C,
∵△DEC∽△BMC,
∴
| DE |
| EC |
| BM |
| MC |
2
| ||||
| 2 |
| 30 |
∵AB∥DC,
∴∠BAD=∠ADM=90°,
∵∠BMD=90°,
∴四边形ABMD为矩形,
∴AB=DM,
∴
 |
| AB |
 |
| DM |
∵
 |
| DM |
 |
| EM |
∴
 |
| AB |
 |
| EM |
∴
 |
| AB |
 |
| EB |
 |
| EM |
 |
| EB |
 |
| AE |
 |
| BM |
∴AE=BM=
| 30 |


练习册系列答案
相关题目







