题目内容
如图,E,F分别是□ABCD的边BA,DC延长线上的点,且AE=CF,EF交AD于G,交BC于H.
(1)图中两对全等的三角形是 ;(不添加任何辅助线)
(2)请在(1)问中选出一对你认为全等的三角形进行证明.
(1)△AEG≌△CFH和△BEH≌△DFG;
(2)如:选择证明△AEG≌△CFH.
证明:在□ABCD 中,∠BAG=∠HCD,
∴ ∠EAG=1800-∠BAG=1800-∠HCD=∠FCH,
又 ∵ BA∥DC, ∴ ∠E=∠F,
又 ∵ AE=CF,∴ △AEG≌△CFH

练习册系列答案
相关题目
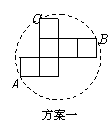
操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:
 | |||
 | |||

纸片利用率=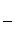 ×100%
×100%
发现:(1)方案一中的点A.B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由.
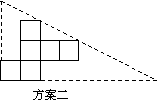
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.
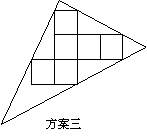
探究:(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.
|
 |
 (x>0)的图象上,且横坐标为2.若将点P先向右平移两个单位,再向上平移一个单位后所得的像为点P′.则在第一象限内,经过点P′的反比例函数图象的解析式是( ).
(x>0)的图象上,且横坐标为2.若将点P先向右平移两个单位,再向上平移一个单位后所得的像为点P′.则在第一象限内,经过点P′的反比例函数图象的解析式是( ).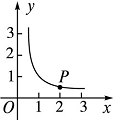
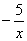 (x>0) B.y=
(x>0) B.y=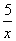 (x>0) C.y=
(x>0) C.y=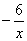 (x>0) D.y=
(x>0) D.y=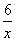 (x>0)
(x>0)

 的
的 顶点坐标是( )
顶点坐标是( )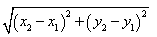 .
.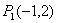 ,
,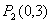 ,
,
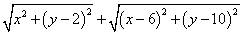 的最小值为 ;
的最小值为 ;

