题目内容
19、如图所示,AE⊥AB,BC⊥CD且AB=AE,BC=CD,F、A、G、C、H在同一直线上,如按照图中所标注的数据及符号,则图中实线所围成的图形面积是

50
.
分析:根据AE⊥AB,BC⊥CD且AB=AE,BC=CD等条件可以证明△AEF≌△ABG,△BCG≌△DCH,即可求出AF、AG、GC、CH的长,然后根据梯形的面积公式和三角形的面积公式即可求出图中实线所围成的图形面积.
解答:解:∵EF⊥FG,BG⊥AC,
∴∠EFA=∠AGB=90°,
∵AE⊥AB且AB=AE,
∴∠EAF=∠ABG,
∴△AEF≌△ABG,
∴AF=BG=3,AG=EF=6,
∵DH⊥CH,BG⊥AC,
∴∠DHC=∠CGB=90°,
∵BC⊥CD且BC=CD,
∴△BCG≌△DCH,
∴GC=DH=4,CH=BG=3,
∴FH=FA+AC+CH=16,
∴图中实线所围成的图形面积S=S直角梯形EFHD-S△EFA-S△ABC-S△CDH
=80-9-15-6=50,
故答案为50.
∴∠EFA=∠AGB=90°,
∵AE⊥AB且AB=AE,
∴∠EAF=∠ABG,
∴△AEF≌△ABG,
∴AF=BG=3,AG=EF=6,
∵DH⊥CH,BG⊥AC,
∴∠DHC=∠CGB=90°,
∵BC⊥CD且BC=CD,
∴△BCG≌△DCH,
∴GC=DH=4,CH=BG=3,
∴FH=FA+AC+CH=16,
∴图中实线所围成的图形面积S=S直角梯形EFHD-S△EFA-S△ABC-S△CDH
=80-9-15-6=50,
故答案为50.
点评:本题主要考查面积及等积变换的知识,解答本题的关键是根据三角形全等求出AF、AG、GC、CH的长,本题比较简单,但是计算时要细心.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
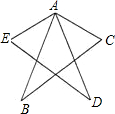 如图所示,AE=AC,AB=AD,∠EAB=∠CAD.求证:∠B=∠D.
如图所示,AE=AC,AB=AD,∠EAB=∠CAD.求证:∠B=∠D.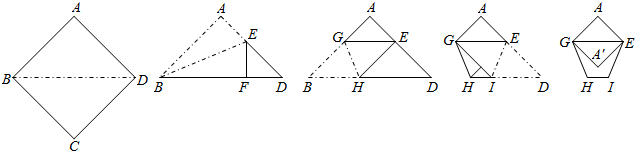
 如图所示,DE⊥AB,DF⊥AC,AE=AF,则下列结论成立的是( )
如图所示,DE⊥AB,DF⊥AC,AE=AF,则下列结论成立的是( ) 如图所示,AE⊥AB,且AE=AB,BC⊥CD且BC=CD,若点E、B、D到直线AC的距离分别为6,3,2,则图中实线所围成的阴影部分面积S是
如图所示,AE⊥AB,且AE=AB,BC⊥CD且BC=CD,若点E、B、D到直线AC的距离分别为6,3,2,则图中实线所围成的阴影部分面积S是