题目内容
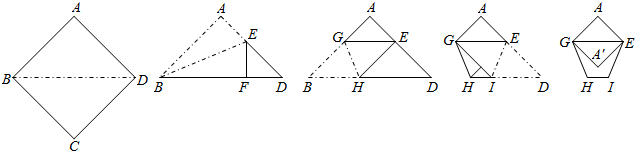
按照图示的方式可以将一张正方形纸片拆成一个环保纸袋(如图所示).AB=
,则折成后纸袋的边AE和HI的长分别为
| 2 |
2-
| 2 |
2-
、| 2 |
6-4
| 2 |
6-4
.| 2 |

分析:在直角△ABD中,利用勾股定理即可求得BD的长,设AE=x,则EF=AE=x,DE=AD-AE=
-x,在直角△EFD中利用勾股定理即可得到一个关于x的方程,解方程求得AE的长;
根据在直角△AEG中利用勾股定理求得GE的长,而ID=BH=BG=GE,根据HI=BD-BH-ID从而求解.
| 2 |
根据在直角△AEG中利用勾股定理求得GE的长,而ID=BH=BG=GE,根据HI=BD-BH-ID从而求解.
解答:解:∵正方形中AB=
,
∴BD=
AB=2,
设AE=x,则EF=AE=x,DE=AD-AE=
-x,
∵△EFD是等腰直角三角形,
∴DE=
EF,即
-x=
x,解得:x=2-
,
即AE=2-
;
∵△AGE是等腰直角三角形,
∴GE=
AE=
(2-
)=2
-2,
∴ID=BH=BG=GE=2
-2,
∴HI=BD-BH-ID=2-2(2
-2)=6-4
.
故答案是:2-
,6-4
.
| 2 |
∴BD=
| 2 |
设AE=x,则EF=AE=x,DE=AD-AE=
| 2 |
∵△EFD是等腰直角三角形,
∴DE=
| 2 |
| 2 |
| 2 |
| 2 |
即AE=2-
| 2 |
∵△AGE是等腰直角三角形,
∴GE=
| 2 |
| 2 |
| 2 |
| 2 |
∴ID=BH=BG=GE=2
| 2 |
∴HI=BD-BH-ID=2-2(2
| 2 |
| 2 |
故答案是:2-
| 2 |
| 2 |
点评:本题考查了图形的折叠问题,正确理解折叠时得到的相等的线段是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 按照图示的方式可以将一张正方形纸片拆成一个环保纸袋(如图所示).
按照图示的方式可以将一张正方形纸片拆成一个环保纸袋(如图所示).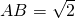 ,则折成后纸袋的边AE和HI的长分别为________、________.
,则折成后纸袋的边AE和HI的长分别为________、________.