题目内容
如图①,一只蚂蚁要从正方体的A顶点出发在这个正方体的表面爬到相距它最远的另一个顶点B,哪条路径最短?说明理由若把正方体改成长方体(如图②),且长方体长、宽、高分别是6cm、4cm、4cm,则哪条路径最短,最短是多少?


答案:
解:

- 考点:
- 两点之间,线段最短,几何体的展开图
- 分析:
本题是一道通过展开平面求最短路径的问题,化空间问题为平面问题是解决空间几何体问题的主要思想.
本题即是利用这一思想,通过“化曲面为平面”解决了“怎样爬行最近”这一几何问题.需要注意的是本题(1)、(2)问中正方体与长方体的不同,不要忘记问题(2)需要分情况讨论这一点.
1、对于第(1)问,根据两点之间线段最短,可知需要通过展开正方体将A、B两点所在的面置于同一平面内;
2、通过展开的图形,连结点A与
B′ 即为最短距离,相信你能得到路径最短的那一条了(因为正方体六个面完全相同,画出一条最短路径即可);【图 2】3、类似问题(1)的思考方法,需要注意长方体与正方体的不同,故第(2)问需要分情况讨论;
4、对经过上表面到达B点与经右侧表面到达B点两种情况进行讨论比较, 求解本问.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,是一块长、宽、高分别是4cm,2cm和1cm的长方体木块、一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
如图,是一块长、宽、高分别是4cm,2cm和1cm的长方体木块、一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )| A、5cm | B、5.4cm | C、6.1cm | D、7cm |
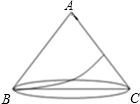 如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少? 如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬一圈回到点B.问:蚂蚁爬行的最短路程是多少?
如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬一圈回到点B.问:蚂蚁爬行的最短路程是多少?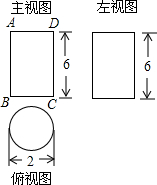 一个几何体的三视图如右图所示,
一个几何体的三视图如右图所示, 如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.若PA=AB=4,∠PAD=30°,有一只蚂蚁要从点P爬到点B,它的最短行程应该是
如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.若PA=AB=4,∠PAD=30°,有一只蚂蚁要从点P爬到点B,它的最短行程应该是