题目内容
(12分)如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),B(4,0),C(0,2)三点
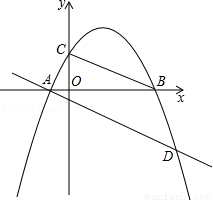
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
(1)y=-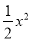 +
+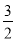 x+2;(2)E点坐标为(0,2),(3,2).
x+2;(2)E点坐标为(0,2),(3,2).
【解析】
试题分析:(1)首先设出函数的解析式,然后利用待定系数法进行求解;(2)首先根据题意判定△ABE只能是以点E为直角顶点的三角形,然后求出BC的长度,根据三角形相似求出点E的坐标.
试题解析:(1)∵抛物线经过点C(0,2) ∴设该抛物线的解析式为y=a +bx+2
+bx+2
将A、B两点坐标代入解析式得: 解得:
解得:
∴抛物线的解析式为:y=-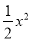 +
+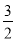 x+2
x+2
(2)存在
由图象可知,以A、B为直角顶点的△ABE不存在,所以△ABE只可能
是以点E为直角顶点的三角形.

在Rt△BOC中,OC=2,OB=4, ∴BC= =
=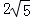 .
.
在Rt△BOC中,设BC边上的高为h,则 ×
×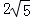 h=
h= ×2×4, ∴h=
×2×4, ∴h=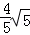 .
.
∵△BEA∽△COB,设E点坐标为(x,y), ∴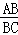 =
= ,∴y=±2
,∴y=±2
将y=2代入抛物线y=-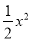 +
+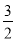 x+2,得
x+2,得 =0,
=0,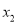 =3.
=3.
当y=﹣2时,不合题意舍去.
∴E点坐标为(0,2),(3,2).
考点:待定系数法求函数解析式、三角形相似的应用.
考点分析: 考点1:二次函数 定义:一般地,如果
 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。 ①所谓二次函数就是说自变量最高次数是2;
②二次函数
 (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。③二次函数
 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式: (1)一般式:
 (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0); (2)顶点式:
 (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0) (3)当抛物线
 与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。 二次函数的一般形式的结构特征:
①函数的关系式是整式;
②自变量的最高次数是2;
③二次项系数不等于零。 二次函数的判定:
二次函数的一般形式中等号右边是关于自变量x的二次三项式;
当b=0,c=0时,y=ax2是特殊的二次函数;
判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成
 (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目

 有意义的x的取值范围是 .
有意义的x的取值范围是 .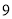 名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前
名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前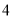 名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这
名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这 .
. -9x = .
-9x = .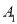 、
、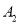 分别代表两张笑脸,
分别代表两张笑脸,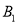 、
、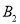 、
、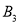 分别代表三张哭脸)
分别代表三张哭脸) 、
、 ,规定
,规定 ,若
,若 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.