Question

5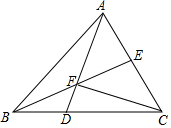．如图，D在△ABC的边BC上，DC=2BD，连接AD与△ABC的中线BE交于点F，连接CF，若△ABC的面积为24，则△AEF的面积为（　　）

• A． 4
• B． 5
• C． 6
• D． 7

Answer 1

分析 过D作DH∥AC交BE于H，根据已知条件得到DH=$\frac{1}{3}$CE，求得DH=$\frac{1}{3}$AE，根据相似三角形的性质得到$\frac{DF}{AF}$=$\frac{DH}{AE}$=$\frac{1}{3}$，求得S_△ABD=$\frac{1}{3}$S_△ABC=8，于是得到结论．

解答 解：过D作DH∥AC交BE于H，
∵DC=2BD，
∴DH=$\frac{1}{3}$CE，
∵AE=CE，
∴DH=$\frac{1}{3}$AE，
∵DH∥AE，
∴△DFH∽△AFE，
∴$\frac{DF}{AF}$=$\frac{DH}{AE}$=$\frac{1}{3}$，
∵△ABC的面积为24，
∴S_△ABD=$\frac{1}{3}$S_△ABC=8，
∴S_△BDF=$\frac{1}{4}$S_△ABD=2，
∴S_△CDF=2S_△BDF=4，
∴S_△AEF=$\frac{1}{2}$（16-4）=6，
故选C．

点评 本题考查了三角形的面积的计算，行线分线段成比例的推论、相似三角形的判定、相似三角形的面积比等于相似比的平方．关键是作辅助线，所作的平行线能用到两个三角形中．