题目内容
已知:在纸面上有一数轴,如图所示,点O为原点,点A1、A2、A3、…分别表示有理数1、2、3、…,点B1、
B2、B3、…分别表示有理数-1、-2、-3、….
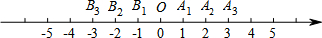
(1)折叠纸面:
①若点A1与点B1重合,则点B2与点 重合;
②若点B1与点A2重合,则点A5与有理数 对应的点重合;
③若点B1与A3重合,当数轴上的M、N(M在N的左侧)两点之间的距离为9,且M、N两点经折叠后重合时,则M、N两点表示的有理数分别是 , ;
(2)拓展思考:
点A在数轴上表示的有理数为a,用|a|表示点A到原点O的距离.
①|a-1|是表示点A到点 的距离;
②若|a-1|=3,则有理数a= ;
③若|a-1|+|a+2|=5,则有理数a= .
B2、B3、…分别表示有理数-1、-2、-3、….
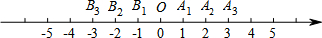
(1)折叠纸面:
①若点A1与点B1重合,则点B2与点
②若点B1与点A2重合,则点A5与有理数
③若点B1与A3重合,当数轴上的M、N(M在N的左侧)两点之间的距离为9,且M、N两点经折叠后重合时,则M、N两点表示的有理数分别是
(2)拓展思考:
点A在数轴上表示的有理数为a,用|a|表示点A到原点O的距离.
①|a-1|是表示点A到点
②若|a-1|=3,则有理数a=
③若|a-1|+|a+2|=5,则有理数a=
考点:数轴,绝对值
专题:
分析:(1)①根据中心对称,可得对称中心,根据对称中心,可得点的对应点;
②根据中心对称,可得对称中心,根据对称中心,可得点的对应点;
③根据中心对称,可得对称中心,根据对称中心到任意一点的距离相等,可得点的对应点;
(2)①根据两点间的距离公示,可得答案;
②根据数轴上到一点距离相等点有两个,位于该点的左右,可得答案;
③根据解含绝对值符号的一元一次方程,可得方程的解.
②根据中心对称,可得对称中心,根据对称中心,可得点的对应点;
③根据中心对称,可得对称中心,根据对称中心到任意一点的距离相等,可得点的对应点;
(2)①根据两点间的距离公示,可得答案;
②根据数轴上到一点距离相等点有两个,位于该点的左右,可得答案;
③根据解含绝对值符号的一元一次方程,可得方程的解.
解答:解:(1)折叠纸面:
①若点A1与点B1重合,则点B2与点 A2重合;
②若点B1与点A2重合,则点A5与有理数 B4对应的点重合;
③若点B1与A3重合,当数轴上的M、N(M在N的左侧)两点之间的距离为9,且M、N两点经折叠后重合时,则M、N两点表示的有理数分别是-3.5,5.5;
(2)拓展思考:
点A在数轴上表示的有理数为a,用|a|表示点A到原点O的距离.
①|a-1|是表示点A到点 A1的距离;
②若|a-1|=3,则有理数a=-2或4;
③若|a-1|+|a+2|=5,则有理数a=-3或 2,
故答案为:A2,B4-3.5,5.5,A1,-2或4,-3或2.
①若点A1与点B1重合,则点B2与点 A2重合;
②若点B1与点A2重合,则点A5与有理数 B4对应的点重合;
③若点B1与A3重合,当数轴上的M、N(M在N的左侧)两点之间的距离为9,且M、N两点经折叠后重合时,则M、N两点表示的有理数分别是-3.5,5.5;
(2)拓展思考:
点A在数轴上表示的有理数为a,用|a|表示点A到原点O的距离.
①|a-1|是表示点A到点 A1的距离;
②若|a-1|=3,则有理数a=-2或4;
③若|a-1|+|a+2|=5,则有理数a=-3或 2,
故答案为:A2,B4-3.5,5.5,A1,-2或4,-3或2.
点评:本题考查了数轴,利用了中心对称的性质,解含绝对值符号的一元一次方程.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
4a-a的计算结果是( )
| A、3 | B、3a | C、4 | D、4a |
-5的倒数是( )
| A、5 | ||
B、
| ||
C、-
| ||
| D、-5 |
 如图,在一个直角边长分别为10米、30米的三角形花园旁边有一个正方形的运动场,这个运动场的面积是
如图,在一个直角边长分别为10米、30米的三角形花园旁边有一个正方形的运动场,这个运动场的面积是 在Rt△ABC中,∠C=90°,BC=8,S△ABC=24,求斜边AB上的高.
在Rt△ABC中,∠C=90°,BC=8,S△ABC=24,求斜边AB上的高.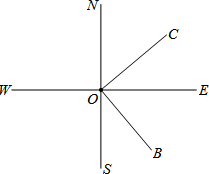 如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.