题目内容
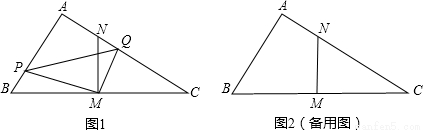
在△ABC中,∠BAC=90°,AB<AC,M是BC边的中点,MN⊥BC交AC于点N.动点P从点B出发沿射线BA以每秒 厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ⊥MP.设运动时间为t秒(t>0).
厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ⊥MP.设运动时间为t秒(t>0).(1)△PBM与△QNM相似吗?以图1为例说明理由;
(2)若∠ABC=60°,AB=
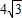 厘米.
厘米.①求动点Q的运动速度;
②设△APQ的面积为S(平方厘米),求S与t的函数关系式;
(3)探求BP2、PQ2、CQ2三者之间的数量关系,以图1为例说明理由.
【答案】分析:(1)通过垂直的定义、直角三角形中的两个锐角互余以及等量代换,可以证得△PBM与△QNM中的两个角对应相等,所以这两个三角形一定相似;
(2)①若BP=3,根据△PBM∽△QNM的对应边成比例可以求得NQ的长,即Q一分钟移动的距离,即点Q的速度;
②分别用时间t表示出AP,AQ的长,根据直角三角形的面积即可求得函数解析式.注意需要分类讨论:当0<t<4时,AP=AB-BP=4 -
- t,AQ=AN+NQ=AC-NC+NQ=12-8+t=4+t,然后由三角形的面积公式可以求得该函数关系式;当t≥4时,AP=
t,AQ=AN+NQ=AC-NC+NQ=12-8+t=4+t,然后由三角形的面积公式可以求得该函数关系式;当t≥4时,AP= t-4
t-4 ,AQ=4+t,然后由三角形的面积公式可以求得该函数关系式;
,AQ=4+t,然后由三角形的面积公式可以求得该函数关系式;
(3)PQ2=BP2+CQ2.作辅助线延长QM至点D,使MD=MQ.连接PD、BD构建平行四边形BDCQ.根据平行四边形的对边平行且相等推知BD∥CQ,BD=CQ;然后在直角三角形BPD中利用勾股定理求得PD2=BP2+BD2=BP2+CQ2;最后利用线段垂直平分线的性质知PQ=PD,所以由等量代换证得该结论.
解答:解:(1)△PBM∽△QNM.理由如下:
如图1,∵MQ⊥MP,MN⊥BC(已知),
∴∠PMB+∠PMN=90°,∠QMN+∠PMN=90°,
∴∠PMB=∠QMN(等量代换).
∵∠PBM+∠C=90°(直角三角形的两个锐角互余),∠QNM+∠C=90°(直角三角形的两个锐角互余),
∴∠PBM=∠QNM(等量代换).
∴△PBM∽△QNM;

(2)∵∠BAC=90°,∠ABC=60°,
∴BC=2AB=8 cm.
cm.
又∵MN垂直平分BC,
∴BM=CM=4 cm.
cm.
∵∠C=30°,
∴MN= CM=4cm;
CM=4cm;
①设Q点的运动速度为vcm/s.
如图1,当0<t<4时,由(1)知△PBM∽△QNM.
∴ (相似三角形的对应边成比例),即
(相似三角形的对应边成比例),即 =
= ,
,
∴v=1;
如图2,当t≥4时,同理可得v=1.
综上所述,Q点运动速度为1cm/s.
②∵AN=AC-NC=12-8=4cm,
∴如图1,当0<t<4时,AP=AB-BP=4 -
- t,AQ=AN+NQ=AC-NC+NQ=12-8+t=4+t,
t,AQ=AN+NQ=AC-NC+NQ=12-8+t=4+t,
∴S= AP•AQ=
AP•AQ= (4
(4 -
- t)(4+t)=-
t)(4+t)=- t2+8
t2+8 ;
;
如图2,当t≥4时,AP= t-4
t-4 ,AQ=4+t,
,AQ=4+t,
∴S= AP•AQ=
AP•AQ= (
( t-4
t-4 )(4+t)=
)(4+t)= t2-8
t2-8 ;
;
综上所述,S= ;
;
(3)PQ2=BP2+CQ2.
证明如下:如图1,延长QM至点D,使MD=MQ.连接PD、BD,BQ,CD
∵BC、DQ互相平分,
∴四边形BDCQ为平行四边形,
∴BD∥CQ,BD=CQ(平行四边形的对边平行且相等);
又∵∠BAC=90°,
∴∠PBD=90°,
∴PD2=BP2+BD2=BP2+CQ2,
∵PM垂直平分DQ,
∴PQ=PD,
∴PQ2=BP2+CQ2.
点评:本题考查了相似三角形的判定与性质,以及相似三角形与函数的综合应用,利用时间t正确表示出题目中线段的长度是解题的关键.
(2)①若BP=3,根据△PBM∽△QNM的对应边成比例可以求得NQ的长,即Q一分钟移动的距离,即点Q的速度;
②分别用时间t表示出AP,AQ的长,根据直角三角形的面积即可求得函数解析式.注意需要分类讨论:当0<t<4时,AP=AB-BP=4
 -
- t,AQ=AN+NQ=AC-NC+NQ=12-8+t=4+t,然后由三角形的面积公式可以求得该函数关系式;当t≥4时,AP=
t,AQ=AN+NQ=AC-NC+NQ=12-8+t=4+t,然后由三角形的面积公式可以求得该函数关系式;当t≥4时,AP= t-4
t-4 ,AQ=4+t,然后由三角形的面积公式可以求得该函数关系式;
,AQ=4+t,然后由三角形的面积公式可以求得该函数关系式;(3)PQ2=BP2+CQ2.作辅助线延长QM至点D,使MD=MQ.连接PD、BD构建平行四边形BDCQ.根据平行四边形的对边平行且相等推知BD∥CQ,BD=CQ;然后在直角三角形BPD中利用勾股定理求得PD2=BP2+BD2=BP2+CQ2;最后利用线段垂直平分线的性质知PQ=PD,所以由等量代换证得该结论.
解答:解:(1)△PBM∽△QNM.理由如下:
如图1,∵MQ⊥MP,MN⊥BC(已知),
∴∠PMB+∠PMN=90°,∠QMN+∠PMN=90°,
∴∠PMB=∠QMN(等量代换).
∵∠PBM+∠C=90°(直角三角形的两个锐角互余),∠QNM+∠C=90°(直角三角形的两个锐角互余),
∴∠PBM=∠QNM(等量代换).
∴△PBM∽△QNM;

(2)∵∠BAC=90°,∠ABC=60°,
∴BC=2AB=8
 cm.
cm.又∵MN垂直平分BC,
∴BM=CM=4
 cm.
cm.∵∠C=30°,
∴MN=
 CM=4cm;
CM=4cm;①设Q点的运动速度为vcm/s.
如图1,当0<t<4时,由(1)知△PBM∽△QNM.
∴
 (相似三角形的对应边成比例),即
(相似三角形的对应边成比例),即 =
= ,
,∴v=1;
如图2,当t≥4时,同理可得v=1.
综上所述,Q点运动速度为1cm/s.
②∵AN=AC-NC=12-8=4cm,
∴如图1,当0<t<4时,AP=AB-BP=4
 -
- t,AQ=AN+NQ=AC-NC+NQ=12-8+t=4+t,
t,AQ=AN+NQ=AC-NC+NQ=12-8+t=4+t,∴S=
 AP•AQ=
AP•AQ= (4
(4 -
- t)(4+t)=-
t)(4+t)=- t2+8
t2+8 ;
;如图2,当t≥4时,AP=
 t-4
t-4 ,AQ=4+t,
,AQ=4+t,∴S=
 AP•AQ=
AP•AQ= (
( t-4
t-4 )(4+t)=
)(4+t)= t2-8
t2-8 ;
;综上所述,S=
 ;
;(3)PQ2=BP2+CQ2.
证明如下:如图1,延长QM至点D,使MD=MQ.连接PD、BD,BQ,CD
∵BC、DQ互相平分,
∴四边形BDCQ为平行四边形,
∴BD∥CQ,BD=CQ(平行四边形的对边平行且相等);
又∵∠BAC=90°,
∴∠PBD=90°,
∴PD2=BP2+BD2=BP2+CQ2,
∵PM垂直平分DQ,
∴PQ=PD,
∴PQ2=BP2+CQ2.
点评:本题考查了相似三角形的判定与性质,以及相似三角形与函数的综合应用,利用时间t正确表示出题目中线段的长度是解题的关键.

练习册系列答案
相关题目
 ;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.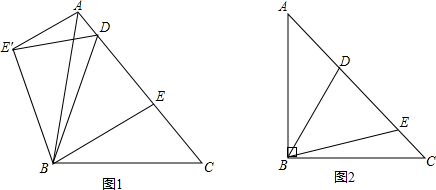
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.