题目内容
在Rt△AOB中,∠AOB=90°,∠ABO=30°,BO=4,分别以OA、OB边所在的直线建立平面直角坐标系,D点为x轴正半轴上的一点,以OD为一边在第一象限内作等边△ODE.
(1)如图12-1,当E点恰好落在线段AB上,求E点坐标;
(2)在(1)问的条件下,将△ODE在线段OB上向右平移,如图12-2,线段EF与线段OO′始终相等吗?请证明你的结论;
(3)若点D从原点出发沿x轴正方向移动,设点D到原点的距离为x,△ODE与△AOB重叠部分的面积为y.当![]() 时,请直接写出y与x的函数关系式.
时,请直接写出y与x的函数关系式.


解:(1)设OD=![]() ,(
,(![]() )过E作EH⊥OD于H, 1分
)过E作EH⊥OD于H, 1分
在Rt△OEH中,![]() ,
,
OE =![]() 2分
2分
∴ E点坐标为(![]() ,
,![]() ). 3分
). 3分
∵ ∠ABO=30°,∠ODE=60°,
∴ ∠DEB=30°.
∴ ∠OEB=90°.
∵ BC=4,∴ OE=a=2. 5分
∴ E(1,![]() ). 6分
). 6分
(2)EF=OO′. 7分
理由如下:
∵ ∠ABO=30°,∠EDO=60°,
∴ ∠ABO=∠DFB=30°.
∴ DF=DB. 9分
∴OO′=OB - DO′- DB
= 4-2-DB
=2-DB
=2-DF
=ED-FD
=EF. 10分
(3)![]() .
.

 如图所示,在Rt△AOB中,点A是直线y=x+m与双曲线y=
如图所示,在Rt△AOB中,点A是直线y=x+m与双曲线y=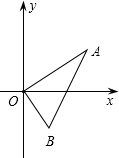 完成下列各题:
完成下列各题:
 如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数
如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程