题目内容
已知：如图，在△AOB中，OA⊥OB，OC⊥AB于C，OB=
cm，OA=
cm，以O为圆心4cm为半径作⊙O．求证：AB与⊙O相切．
证明：在△AOB中，OA⊥OB，OC⊥AB于C，OB=cm，OA=cm，
∴AB=
=
=10，
∵
OA•OB=AB•OC，
∴OA•OB=AB•OC，
即×=10•OC，
解得OC=4，
∵⊙O半径为4cm，OC⊥AB于C，
∴AB与⊙O相切．
分析：在直角三角形BOA中，利用勾股定理求得AB=10，由面积相等得OA•OB=AB•OC，即×=10•OC，得OC=4，即⊙O经过点C，且OC⊥AB，所以AB与⊙O相切．
点评：本题考查了切线的判定定理，本题已知OC⊥AB，因此我们只需证明OC是圆的半径即可．
cm，OA=cm，∴AB=
==10，∵
OA•OB=AB•OC，∴OA•OB=AB•OC，
即
×=10•OC，解得OC=4，
∵⊙O半径为4cm，OC⊥AB于C，
∴AB与⊙O相切．
分析：在直角三角形BOA中，利用勾股定理求得AB=10，由面积相等得OA•OB=AB•OC，即
×=10•OC，得OC=4，即⊙O经过点C，且OC⊥AB，所以AB与⊙O相切．点评：本题考查了切线的判定定理，本题已知OC⊥AB，因此我们只需证明OC是圆的半径即可．
练习册系列答案
相关题目
存在，请说明理由；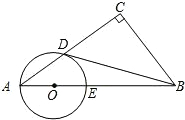
已知：如图，在Rt△ABC中，∠C=90°，点O在AB上，以O为圆心，OA长为半径的圆与AC，AB分别交于点D，E，且∠CBD=∠A．
27、已知：如图，在⊙O中，OA是半径，CD是弦，OA交CD于点E．现有四个条件：①∠COA=∠AOD=60°；②AC=AD=OA；③点E分别是AO、CD的中点；④OA⊥CD．
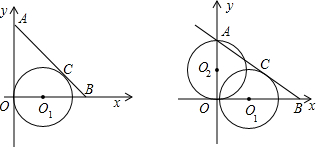P两点，求证：O1M•O1P=2．