题目内容
△ABC的内切圆半径为r，△ABC的周长为l，则△ABC的面积为 ．
【答案】分析：如图，连接圆心和切点，则可得到垂直关系，将图形分割成三个三角形，求三个三角形的面积和即可．
解答：
解：由题意，如图，连接OE，OD，OF；OA，OB，OC；
则OE⊥AB，OF⊥AC，OD⊥BC；
∴△ABC的面积=
AB×OE+
BC×OD+
AC×OF
∵OE=OF=OD=r，AB+BC+AC=l，
∴△ABC的面积=
AB×r+
BC×r+
AC×r=
（AB+BC+AC）
=
l．
点评：本题解答的关键是，充分利用已知条件，将问题转化为求几个三角形面积的和．
解答：
解：由题意，如图，连接OE，OD，OF；OA，OB，OC；则OE⊥AB，OF⊥AC，OD⊥BC；
∴△ABC的面积=
AB×OE+BC×OD+AC×OF∵OE=OF=OD=r，AB+BC+AC=l，
∴△ABC的面积=
AB×r+BC×r+AC×r=（AB+BC+AC）=
l．点评：本题解答的关键是，充分利用已知条件，将问题转化为求几个三角形面积的和．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
如图，Rt△ABC中，∠C=90°，AC=6，BC=8．则△ABC的内切圆半径r=
如图，Rt△ABC中，AC=6，CB=8，则△ABC的内切圆半径r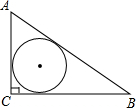为（ ）| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
到目前为止，计算三角形的面积有哪一些公式呢？下面我们来小结归纳一下吧：
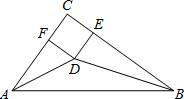（2012•乐山模拟）如图，在△ABC中，∠C=90°，∠A、∠B的平分线交于点D，DE⊥BC于点E，DF⊥AC于点F．
已知△ABC的内切圆半径r=