Question

到目前为止，计算三角形的面积有哪一些公式呢？下面我们来小结归纳一下吧：
公式（1）：s△=

1

2

×底×高
公式（2）：s△=

1

2

•(a+b+c)•r，其中a、b、c为三角形三边长，r为三角形内切圆半径．
公式（3）：课本P19海伦-秦九韶公式：s△=

p(p-a)(p-b)(p-c)

其中a、b、c为三角形三边长，p=

a+b+c

2

根据上述3个公式，请你选择适当的方法计算：
问题1：已知△ABC的三边a=4，b=5，c=6，求△ABC的面积．
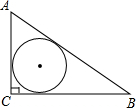
问题2：如图，在Rt△ABC中，∠C=90°，AC=5，BC=12，求△ABC的内切圆半径r．

Answer 1

分析：问题1：由已知△ABC的三边a=4，b=5，c=6，可知这是一个一般的三角形，故选用海伦-秦九韶公式求解；
问题2：由在Rt△ABC中，∠C=90°，AC=5，BC=12，利用勾股定理，可求得AB的长，故选用公式（2）：s△=

1

2

•(a+b+c)•r，其中a、b、c为三角形三边长，r为三角形内切圆半径．

解答：解：问题1：∵a=4，b=5，c=6，
∴p=

a+b+c

2

=

4+5+6

2

=

15

2

，
∴S_△ABC=

p(p-a)(p-b)(p-c)

=

15 2 ( 15 2 -4)( 15 2 -5)( 15 2 -6)

=

15

4

7

；

问题2：∵在Rt△ABC中，∠C=90°，AC=5，BC=12，
∴AB=

AC2+BC2

=13，
∵S_△ABC=

1

2

AC•BC=

1

2

（AB+AC+BC）•r，
∴r=

AC•BC

AC+BC+AB

=2．

点评：此题考查了三角形面积的求解方法．此题难度不大，注意选择适当的求解方法是关键．