题目内容
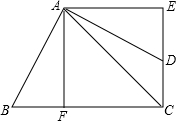 (2013•潍坊二模)如图,正方形AFCE中,D是边CE上一点,B是CF延长线上一点,且AB=AD,若四边形ABCD的面积是24cm2.则AC长是
(2013•潍坊二模)如图,正方形AFCE中,D是边CE上一点,B是CF延长线上一点,且AB=AD,若四边形ABCD的面积是24cm2.则AC长是4
| 3 |
4
cm.| 3 |
分析:证Rt△AED≌Rt△AFB,推出S△AED=S△AFB,根据四边形ABCD的面积是24cm2得出正方形AFCE的面积是24cm2,求出AE、EC的长,根据勾股定理求出AC即可.
解答:解:∵四边形AFCE是正方形,
∴AF=AE,∠E=∠AFC=∠AFB=90°,
∵在Rt△AED和Rt△AFB中
∴Rt△AED≌Rt△AFB(HL),
∴S△AED=S△AFB,
∵四边形ABCD的面积是24cm2,
∴正方形AFCE的面积是24cm2,
∴AE=EC=
=2
(cm),
根据勾股定理得:AC=
=4
,
故答案为:4
.
∴AF=AE,∠E=∠AFC=∠AFB=90°,
∵在Rt△AED和Rt△AFB中
|
∴Rt△AED≌Rt△AFB(HL),
∴S△AED=S△AFB,
∵四边形ABCD的面积是24cm2,
∴正方形AFCE的面积是24cm2,
∴AE=EC=
| 24 |
| 6 |
根据勾股定理得:AC=
(2
|
| 3 |
故答案为:4
| 3 |
点评:本题考查了全等三角形的性质和判定,正方形性质,勾股定理等知识点的应用.关键是求出正方形AFCE的面积.

练习册系列答案
相关题目
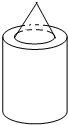 (2013•潍坊二模)如图,组合体的俯视图是( )
(2013•潍坊二模)如图,组合体的俯视图是( ) (2013•潍坊二模)如图,AB的中垂线为CP交AB于点P,且AC=2CP.甲、乙两人想在AB上取D、E两点,使得AD=DC=CE=EB,其作法如下:甲作∠ACP、∠BCP的角平分线,分别交AB于D、E两点,则D、E即为所求;乙作AC、BC的中垂线,分别交AB于D、E两点,则D、E即为所求.对于甲、乙两人的作法,下列正确的是( )
(2013•潍坊二模)如图,AB的中垂线为CP交AB于点P,且AC=2CP.甲、乙两人想在AB上取D、E两点,使得AD=DC=CE=EB,其作法如下:甲作∠ACP、∠BCP的角平分线,分别交AB于D、E两点,则D、E即为所求;乙作AC、BC的中垂线,分别交AB于D、E两点,则D、E即为所求.对于甲、乙两人的作法,下列正确的是( )