题目内容
【题目】已知函数y1=mx2+n,y2=nx+m(mn≠0),则两个函数在同一坐标系中的图象可能为( )
A.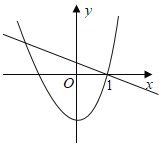 B.
B.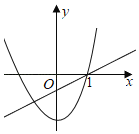
C. D.
D.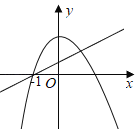
【答案】A
【解析】
可先根据一次函数的图象判断m的符号,再判断二次函数图象与实际是否相符,进而判断选项的正误.
解:A、由一次函数y2=nx+m(mn≠0)的图象可得:n<0,m>0.此时二次函数y1=mx2+n的图象应该开口向上,抛物线与y轴交于负半轴,故选项符合题意;
B、由一次函数y2=nx+m(mn≠0)的图象可得:n>0,m<0.此时二次函数y1=mx2+n的图象应该开口向下,抛物线与y轴交于正半轴,故本选项不符合题意;
C、由一次函数y2=nx+m(mn≠0)的图象可得:n<0,m<0.此时二次函数y1=mx2+n的图象应该开口向下,抛物线与y轴交于负半轴,故本选项不符合题意;
D、由一次函数y2=nx+m(mn≠0)的图象可得:n>0,m>0.此时二次函数y1=mx2+n的图象开口向上,抛物线与y轴交于正半轴,故本选项不符合题意;
故选:A.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
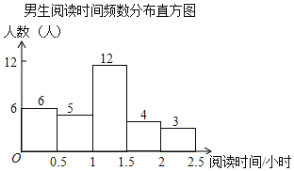
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,![]() ,
,![]() ;
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?
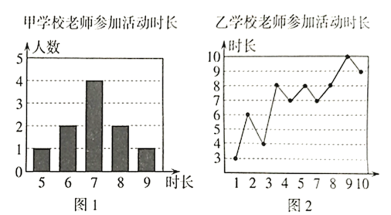
【题目】甲、乙两所学校选派相同人数的老师参加志愿者活动,參加活动时长分别被制成下列两个统计图,根据以上信息,整理分析数据如下表:
平均时间/小时 | 中位数/小时 | 众数/小时 | 方差/小时 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
![]() 求出表格中
求出表格中![]() 的值.
的值.
![]() 分别运用表中的统计量,简要分析这两所学校参加志愿者活动的时长,若选其中一所学校作为志愿推广学校,你认为应该选哪所?
分别运用表中的统计量,简要分析这两所学校参加志愿者活动的时长,若选其中一所学校作为志愿推广学校,你认为应该选哪所?