题目内容
 将正方形ABCD绕点A按逆时针方向旋转n°(0<n<90),得正方形AB1C1D1,B1C1交CD于点E.
将正方形ABCD绕点A按逆时针方向旋转n°(0<n<90),得正方形AB1C1D1,B1C1交CD于点E.(1)求证:B1E=DE;
(2)简要说明四边形AB1ED存在一个内切圆;
(3)若n=30(度),AB=
| 3 |
分析:(1)根据旋转的性质及三角形全等的性质,即可得出结论.
(2)根据(1)的结论及由四边形有内切圆时应满足的条件,可判断出四边形AB1ED存在一个内切圆.
(3)由(2)可知,四边形AB1ED存在一个内切圆,所以此圆的圆心一定在四个角平分线的交点上,作∠DAF与∠AB1G的角平分线交于点O,则O即为该圆的圆心,过O作OF⊥AB1,n=30°,AB=
,再根据直角三角形的性质便可求出OF的长,即该四边形内切圆的圆心.
(2)根据(1)的结论及由四边形有内切圆时应满足的条件,可判断出四边形AB1ED存在一个内切圆.
(3)由(2)可知,四边形AB1ED存在一个内切圆,所以此圆的圆心一定在四个角平分线的交点上,作∠DAF与∠AB1G的角平分线交于点O,则O即为该圆的圆心,过O作OF⊥AB1,n=30°,AB=
| 3 |
解答: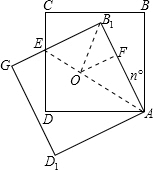 解:(1)连接AE,
解:(1)连接AE,
由旋转的性质可知在AD=AB1,
Rt△AED与Rt△AEB1中,AE=AE,AD=AB1,
∴Rt△AED≌Rt△AEB1,
故B1E=DE.
(2)由(1)可知,Rt△AED≌Rt△AEB1,
∴EB1+AD=ED+AB1,
故四边形AB1ED存在一个内切圆.
(3)作∠DAF与∠AB1G的角平分线交于点O,过O作OF⊥AB1,
则∠OAF=n=30°,∠AB1O=45°,
故B1F=OF=
OA,
设B1F=x,则AF=
-x,
故(
-x)2+x2=(2x)2,
解得x=
或x=
(舍去).
 解:(1)连接AE,
解:(1)连接AE,由旋转的性质可知在AD=AB1,
Rt△AED与Rt△AEB1中,AE=AE,AD=AB1,
∴Rt△AED≌Rt△AEB1,
故B1E=DE.
(2)由(1)可知,Rt△AED≌Rt△AEB1,
∴EB1+AD=ED+AB1,
故四边形AB1ED存在一个内切圆.
(3)作∠DAF与∠AB1G的角平分线交于点O,过O作OF⊥AB1,
则∠OAF=n=30°,∠AB1O=45°,
故B1F=OF=
| 1 |
| 2 |
设B1F=x,则AF=
| 3 |
故(
| 3 |
解得x=
-
| ||
| 2 |
-
| ||
| 2 |
点评:本题考查的是旋转的性质及园内切四边形成立的条件及性质,要熟练掌握正方形的性质及直角三角形的性质,是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在平面直角坐标系中,O为坐标原点,每个小方格的边长为1个单位长度.正方形ABCD顶点都在格点上,其中,点A的坐标为(1,1).
如图,在平面直角坐标系中,O为坐标原点,每个小方格的边长为1个单位长度.正方形ABCD顶点都在格点上,其中,点A的坐标为(1,1).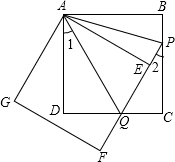 (2013•拱墅区一模)如图,正方形ABCD的边长为3,将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°),得到正方形AEFG,FE交线段DC于点Q,FE的延长线交线段BC于点P,连结AP、AQ.
(2013•拱墅区一模)如图,正方形ABCD的边长为3,将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°),得到正方形AEFG,FE交线段DC于点Q,FE的延长线交线段BC于点P,连结AP、AQ.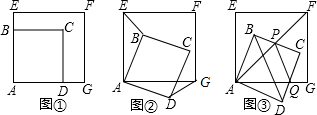
 (2013•南通一模)如图,已知正方形ABCD的边长为a,将正方形ABCD绕点A顺时针旋转45°,则阴影部分的面积为( )
(2013•南通一模)如图,已知正方形ABCD的边长为a,将正方形ABCD绕点A顺时针旋转45°,则阴影部分的面积为( )