题目内容
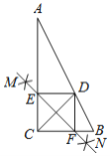
【题目】如图,已知![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 延长线上的动点,过点
延长线上的动点,过点![]() 作
作![]() 的切线
的切线![]() ,
,![]() 为切点,
为切点, ![]() 为
为![]() 上的动点,连接
上的动点,连接![]() 交
交![]() 于点
于点![]() .
.
(1)当![]() 平分
平分![]() 时,求证:
时,求证:![]() ;
;
(2)当![]() 是
是![]() 的中点时,求证:
的中点时,求证:![]() ;
;
(3)当![]() ,且
,且![]() 的周长被
的周长被![]() 平分时,设
平分时,设![]() ,试求
,试求![]() 的值.
的值.
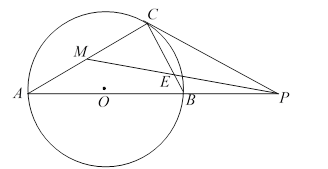
【答案】(1)45°;(2)详见解析;(3)![]()
【解析】
(1)连接![]() .根据切线定义可得:
.根据切线定义可得:![]() ,由角平分线的性质可得:
,由角平分线的性质可得:![]() ,再由等腰三角形的性质和三角形外角的性质可得:
,再由等腰三角形的性质和三角形外角的性质可得:![]() ,根据角的和差即可得出结论;
,根据角的和差即可得出结论;
(2)过![]() 作
作![]() 交
交![]() 于
于![]() .由
.由![]() ,得到
,得到![]() ,由相似三角形的性质可得:
,由相似三角形的性质可得:![]() .根据中点的定义及等量代换即可得出结论;
.根据中点的定义及等量代换即可得出结论;
(3)设![]() ,则
,则![]() .由余弦的定义求出∠COP=60°,从而得到△OBC为等边三角形,进而求出BC、AC的长,得到△ABC的周长,根据
.由余弦的定义求出∠COP=60°,从而得到△OBC为等边三角形,进而求出BC、AC的长,得到△ABC的周长,根据![]() 的周长被
的周长被![]() 平分,表示出CE,BE,AM,由(2)知,
平分,表示出CE,BE,AM,由(2)知,![]() ,从而求出
,从而求出![]() .
.
(1)连接![]() .
.
![]() 切
切![]() 于
于![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() .
.
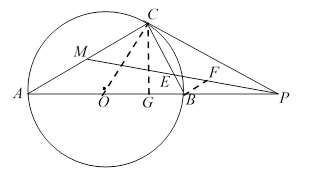
(2)过![]() 作
作![]() 交
交![]() 于
于![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,
(3)设![]() ,则
,则![]() .
.
![]() ,
,
![]() ,
,![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() .
.
![]()
![]() 的周长被
的周长被![]() 平分,
平分,![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,
由(2)知,![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,即
,即![]() .
.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目