题目内容
(本题满分10分)某剧院举行专场音乐会,成人票每张20元,学生票每张5元,暑假期间,为了丰富广大师生的业余文化生活,剧院制定了两种优惠方案,方案一:购买一张成人票赠送一张学生票;方案二:按总价的90%付款,某校有4名老师与若干名(不少于4人)学生听音乐会.
(1)设学生人数为x(人),分别求出方案一、方案二的付款总金额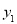 、
、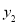 (元)与x的函数表达式;
(元)与x的函数表达式;
(2)学生人数在什么范围内,两种方案费用一样?人数在什么范围内,选方案一较划算?人数在什么范围内,选方案二较划算?
(1)y1=20×4+(x﹣4)×5=5x+60(x≥4),y2=(5x+20×4)×90%=4.5x+72(x≥4);
(2)当购买24张票时,两种优惠方案付款一样多;当4≤x<24时,y1<y2,选方案一较划算;当x>24时,y1>y2,选方案二较划算.
【解析】
试题分析:(1)由题意得方案1:y=4个成人总花费+(x-4)个学生的总花费;方案2:y=(4个成人总花费+x个学生的总花费)×90%;
(2)分情况讨论,①当y1﹣y2=0时,②当y1﹣y2<0时,③当y1﹣y2>0时,分别根据(1)中的解析式构造不等式,解得x的范围.
试题解析:【解析】
(1)按优惠方案一可得,
y1=20×4+(x﹣4)×5=5x+60(x≥4),
按优惠方案二可得,
y2=(5x+20×4)×90%=4.5x+72(x≥4);
(2)因为y1﹣y2=0.5x﹣12(x≥4),
①当y1﹣y2=0时,得0.5x﹣12=0,解得x=24,
∴当购买24张票时,两种优惠方案付款一样多.
②当y1﹣y2<0时,得0.5x﹣12<0,解得x<24,
∴当4≤x<24时,y1<y2,选方案一较划算.
③当y1﹣y2>0时,得0.5x﹣12>0,解得x>24,
当x>24时,y1>y2,选方案二较划算.
(注:学生没写x≥4,不扣分)
考点:一次函数应用题.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案 的图象与x轴有交点,求k的取值范围.
的图象与x轴有交点,求k的取值范围.
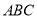 ≌△
≌△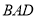 .
.