题目内容
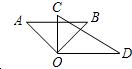 26、将两副三角板的两个直角的顶点O重合在一起,放置成如图所示的位置.
26、将两副三角板的两个直角的顶点O重合在一起,放置成如图所示的位置.(1)如果重叠在一起∠BOC=60°,猜想∠AOD=
120°
;(2)如果重叠在一起∠BOC=80°,猜想∠AOD=
100°
;(3)猜想∠AOD+∠BOC=
180°
;(4)由此可知三角板AOB绕重合点O旋转,不论旋转到任何位置,∠AOD与∠BOC始终满足
∠AOD+∠BOC=180°
关系.分析:(1)、(2)均利用∠AOD=∠AOB+∠COD-∠BOC得到∠AOD,故(3)可猜想∠AOD+∠BOC=180°,(4)设∠BOC=α,∠AOD+∠BOC=∠AOB+∠BOD+∠BOC=∠AOB+∠COD=180°,故可得到结论.
解答:解:(1)由∠AOD=∠AOB+∠COD-∠BOC,
当∠BOC=60°,
∴∠AOD=120°,
(2)由(1)知,∠AOD=100°,
(3)猜想∠AOD+∠BOC=180°,
(4)设∠BOC=α,
∠AOD+∠BOC=∠AOB+∠BOD+∠BOC=∠AOB+∠COD=180°,
故∠AOD+∠BOC=180°.
当∠BOC=60°,
∴∠AOD=120°,
(2)由(1)知,∠AOD=100°,
(3)猜想∠AOD+∠BOC=180°,
(4)设∠BOC=α,
∠AOD+∠BOC=∠AOB+∠BOD+∠BOC=∠AOB+∠COD=180°,
故∠AOD+∠BOC=180°.
点评:本题主要考查角的比较与运算,充分利用∠AOD=∠AOB+∠COD-∠BOC解答此题.

练习册系列答案
相关题目

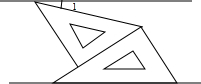 (2013•盘锦)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
(2013•盘锦)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )