题目内容
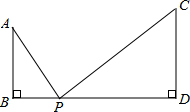 如图,AB⊥BD,CD⊥BD,AB=6,CD=16,BD=20,一动点P从B向D运动,问当P离B多远时,△PAB与△PCD是相似三角形?试求出所有符合条件的P点的位置.
如图,AB⊥BD,CD⊥BD,AB=6,CD=16,BD=20,一动点P从B向D运动,问当P离B多远时,△PAB与△PCD是相似三角形?试求出所有符合条件的P点的位置.
解:设BP=x,BD=20,则PD=BD-BP=20-x,
分两种情况考虑:
假设△PAB∽△PCD,有 =
=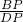 ,
,
又AB=6,CD=16,
∴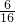 =
= ,即6(20-x)=16x,
,即6(20-x)=16x,
解得:x=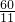 ;
;
假设△PAB∽△CPD,有 =
= ,
,
∴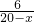 =
=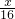 ,即x(20-x)=96,
,即x(20-x)=96,
整理得:(x-12)(x-8)=0,
解得:x1=12,x2=8,
综上,当P离B的距离为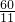 或8或12时,△PAB与△PCD是相似三角形.
或8或12时,△PAB与△PCD是相似三角形.
分析:设BP=x,由BD-BP表示出PD,分两种情况考虑:当△PAB∽△PCD时;当△PAB∽△CPD时,分别由相似得比例,将各自的值代入列出关于x的方程,求出方程的解得到x的值,即为PB的长.
点评:此题考查了相似三角形的判定,利用了分类讨论的思想,相似三角形的判定方法为:两对对应角相等的两三角形相似;三边对应成比例的两三角形相似;两边对应成比例且夹角相等的两三角形相似.
分两种情况考虑:
假设△PAB∽△PCD,有
 =
=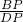 ,
,又AB=6,CD=16,
∴
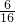 =
= ,即6(20-x)=16x,
,即6(20-x)=16x,解得:x=
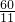 ;
;假设△PAB∽△CPD,有
 =
= ,
,∴
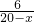 =
=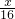 ,即x(20-x)=96,
,即x(20-x)=96,整理得:(x-12)(x-8)=0,
解得:x1=12,x2=8,
综上,当P离B的距离为
 或8或12时,△PAB与△PCD是相似三角形.
或8或12时,△PAB与△PCD是相似三角形.分析:设BP=x,由BD-BP表示出PD,分两种情况考虑:当△PAB∽△PCD时;当△PAB∽△CPD时,分别由相似得比例,将各自的值代入列出关于x的方程,求出方程的解得到x的值,即为PB的长.
点评:此题考查了相似三角形的判定,利用了分类讨论的思想,相似三角形的判定方法为:两对对应角相等的两三角形相似;三边对应成比例的两三角形相似;两边对应成比例且夹角相等的两三角形相似.

练习册系列答案
相关题目
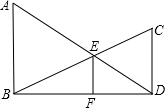 已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明
已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明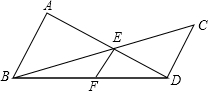
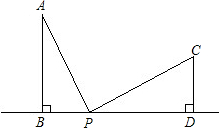 如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在直线BD上,由B点到D点移动,
如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在直线BD上,由B点到D点移动, 如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.
如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED. 如图,AB=BD,BC=BE,∠ABD=∠EBC,则有
如图,AB=BD,BC=BE,∠ABD=∠EBC,则有 如图,AB⊥BD,CD⊥BD,AD=CB.求证:AD∥BC.
如图,AB⊥BD,CD⊥BD,AD=CB.求证:AD∥BC.