题目内容
已知一元二次方程x2-4x+3=0的两根为x1，x2，那么（1+x1）（1+x2）的值是 ．
考点：根与系数的关系
专题：计算题
分析：根据根与系数的关系得到x1+x2=4，x1x2=3，然后把（1+x1）（1+x2）展开得到1+x1+x2+x1x2，然后利用整体代入的方法计算．
解答：解：根据题意得x1+x2=4，x1x2=3，
所以（1+x1）（1+x2）=1+x1+x2+x1x2=1+4+3=8．
故答案为8．
所以（1+x1）（1+x2）=1+x1+x2+x1x2=1+4+3=8．
故答案为8．
点评：本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-
，x1x2=
．
| b |
| a |
| c |
| a |
练习册系列答案
53随堂测系列答案
相关题目
有若干根火柴棍，其长为1，摆成如图一系列三角形图案，按这种方式摆下去，它的规律是什么？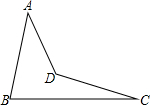
（1）如图，四边形ABCD中，∠A=30°，∠B=60°，∠C=20°，则∠ADC=