题目内容
如右图,点A(1,6)和点M(m,n)都在反比例函数y= k (k>0)的图像上.
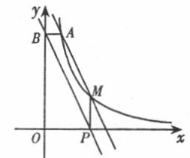
(1)求k的值;
(2)当m=3时,求直线AM的解析式;
(3)当m>1时,过点M作MP上x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.
解:(1)点A(1,6)在反比例函数y=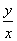 (k>o)的图像上,所以k=xy=6………………2分
(k>o)的图像上,所以k=xy=6………………2分
(2)当m=3时,则n=2,所以M(3,2)……………3分
设直线AM的解析式为y=kx+b
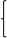 6=k+b
6=k+b
则 2=3k+b …………4分
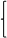 解得k=-2
解得k=-2
B=8
所以直线AM的解析式为y=-2x+8……………………5分
(3)延长BA、PM相交于N则∠N =90°…………………6分
∵A(1,6),M(m,n)
∴B(0,6),P(m,0),N(m,6)
∴BN=m,PN=6,AN=m-1,MN=6-n……………… 7分
∴tan∠1= =
=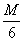 , tan∠2=
, tan∠2= 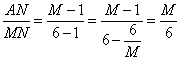
∴tan∠1=tan∠2……………… 8分
∴∠1=∠2
∴AM//BP………………………………9分

练习册系列答案
相关题目
 B.
B. 或一
或一
 00007克,用科学记数法表示此数正确的是( )
00007克,用科学记数法表示此数正确的是( ) B.
B.  C.
C.  D.
D. 
 的值为9,则
的值为9,则 的值为( )
的值为( )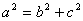 ,则该三角形是直角三角形;②若
,则该三角形是直角三角形;②若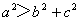 ,则该三角形是钝角三角形;③
,则该三角形是钝角三角形;③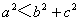 ,则该三角形是锐角三角形
,则该三角形是锐角三角形 ,故由上
,故由上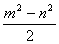 ,
,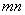 ,
,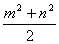 请判断这个三角形的形状,并写出你的判断过程
请判断这个三角形的形状,并写出你的判断过程