题目内容
 (2012•甘孜州)已知:如图,在?ABCD中,O为对角线的中点.过O的直线MN交AB边于点M,交CD边于点N;过O的另一条直线PQ交AD边于点P,交BC边于点Q,连接PN,MQ.证明:△PON与△QOM全等.
(2012•甘孜州)已知:如图,在?ABCD中,O为对角线的中点.过O的直线MN交AB边于点M,交CD边于点N;过O的另一条直线PQ交AD边于点P,交BC边于点Q,连接PN,MQ.证明:△PON与△QOM全等.分析:由在?ABCD中,O为对角线线的中点,易证得△POD≌△QOB,则可得OP=OQ,同理可得ON=OM,然后由SAS证得:△PON与△QOM全等.
解答:证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠PDO=∠QBO,
在△POD和△QOB中,
,
∴△POD≌△QOB(ASA),
∴OP=OQ,
同理:ON=OM,
在△PON和△QOM中,
,
∴△PON≌△QOM(SAS).
∴AD∥BC,
∴∠PDO=∠QBO,
在△POD和△QOB中,
|
∴△POD≌△QOB(ASA),
∴OP=OQ,
同理:ON=OM,
在△PON和△QOM中,
|
∴△PON≌△QOM(SAS).
点评:此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•甘孜州)如图放置的圆锥,它的主视图、俯视图、左视图分别为( )
(2012•甘孜州)如图放置的圆锥,它的主视图、俯视图、左视图分别为( )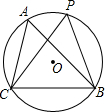 (2012•甘孜州)如图.⊙O是△ABC的外接圆,∠CAB=65°,P是⊙O上的一点,则∠CPB等于( )
(2012•甘孜州)如图.⊙O是△ABC的外接圆,∠CAB=65°,P是⊙O上的一点,则∠CPB等于( ) (2012•甘孜州)如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )
(2012•甘孜州)如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )