题目内容
已知:如图,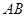 是⊙O的直径,点
是⊙O的直径,点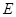 是
是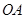 上任意一点,过点
上任意一点,过点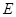 作弦
作弦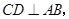 点
点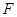 是
是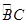 上任一点,连结
上任一点,连结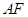 交
交 于
于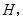 连结AC、CF、BD、OD.
连结AC、CF、BD、OD.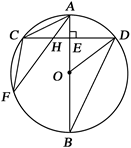
【小题1】 (1)求证:
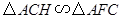 ;
;【小题2】(2)猜想:
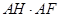 与
与 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;【小题3】 (3)试探究:当点
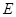 位于何处时,△
位于何处时,△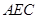 的面积与△
的面积与△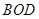 的面积之比为1:2?并加以证明.
的面积之比为1:2?并加以证明.
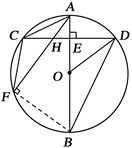
【小题1】(1)证明:∵ 弦CD⊥直径AB于点E, ∴
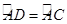 .
. ∴ ∠ACD =∠AFC.
又 ∵ ∠CAH=∠FAC,
∴ △ACH∽△AFC(两角对
 应相等的两个三角形相似).--------------1分
应相等的两个三角形相似).--------------1分【小题2】(2)猜想:AH·AF=AE·AB.
证明:连结FB.
∵ AB为直径,∴ ∠AFB=90°.
又∵ AB⊥CD于点E,∴ ∠AEH=90°.
∴
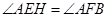 . ∵ ∠EAH=∠FAB,
. ∵ ∠EAH=∠FAB,∴ △AHE∽△ABF.
∴
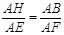 .
.∴ AH·AF=AE·AB.------------------------------------------------- -----3分
【小题3】(3)答:当点
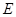 位于
位于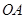 的中点(或
的中点(或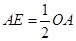 )时,△
)时,△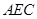 的面积与△
的面积与△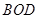 的面积之比为1:2.
的面积之比为1:2.证明:设 △
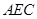 的面积为
的面积为 ,△
,△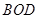 的面积为
的面积为 .
.∵ 弦CD⊥直径AB于点E, ∴
 =
=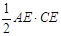 ,
, =
=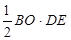 .
.∵
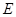 位于
位于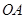 的中点,∴
的中点,∴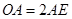 .
.又
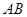 是⊙O的直径,∴
是⊙O的直径,∴ 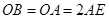 .
.∴
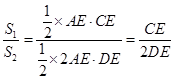 .
.又 由垂径定理知 CE=ED,∴
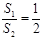 .
.∴ 当点
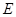 位于
位于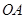 的中点时,△
的中点时,△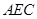 的面积与△
的面积与△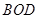 的面
的面积之比为1:2. -
 ------------------------------------------------7分解析:
------------------------------------------------7分解析:略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 22、已知,如图CD是⊙O的切线,C是切点,直径AB的延长线与CD相交于D,连接OC、BC.
22、已知,如图CD是⊙O的切线,C是切点,直径AB的延长线与CD相交于D,连接OC、BC.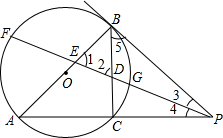 、BC于E、D,交⊙O于F、G,且BE、BD恰好是关于x的方程x2-6x+(m2+4m+13)=0(其中m为实数)的两根.
、BC于E、D,交⊙O于F、G,且BE、BD恰好是关于x的方程x2-6x+(m2+4m+13)=0(其中m为实数)的两根. (2002•西藏)已知,如图AB是⊙O的直径,半径OC⊥AB,弦CD与AB交于点E.
(2002•西藏)已知,如图AB是⊙O的直径,半径OC⊥AB,弦CD与AB交于点E.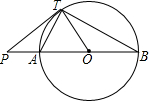 已知:如图PT是⊙O的切线,T为切点,PAB是经过圆心O的割线.
已知:如图PT是⊙O的切线,T为切点,PAB是经过圆心O的割线. 已知,如图DE是△ABC的边AB的垂直平分线,D为垂足,DE交BC于E,且AC=5,BC=8,则△AEC的周长为
已知,如图DE是△ABC的边AB的垂直平分线,D为垂足,DE交BC于E,且AC=5,BC=8,则△AEC的周长为