题目内容
已知：如图AB是⊙O的直径，PB切⊙O于点B，PA交⊙O于点C，PF分别交AB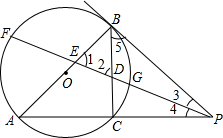
、BC于E、D，交⊙O于F、G，且BE、BD恰好是关于x的方程x2-6x+（m2+4m+13）=0（其中m为实数）的两根．（1）求证：BE=BD．
（2）若GE•EF=6
| 3 |
分析：（1）要证明BE=BD，就要根据BE、BD恰好是关于x的方程x2-6x+（m2+4m+13）=0（其中m为实数）的两根，来判断，是它的两根，可见此方程有根，所以求出△，必须≥0．利用这求出m的值．从而求出这个方程的一般式，然后解方程求出根，即是BE、BD的长度；
（2）要求∠A的度数就要利用直角三角形的角边关系，求出在Rt△ACB中sinA的值，要求sinA的值，就要求BC，AB的值．这就要利用题中给出的条件利用相似三角形来求．
（2）要求∠A的度数就要利用直角三角形的角边关系，求出在Rt△ACB中sinA的值，要求sinA的值，就要求BC，AB的值．这就要利用题中给出的条件利用相似三角形来求．
解答：（1）证明：∵BE、BD是关于x的方程x2-6x+（m2+4m+13）=0的两根，
∴△=（-6）2-4（m2+4m+13）=-4（m+2）2≥0，∴m=-2，（2分）
原方程为x2-6x+9=0，
解之，得x1=x2=3，
∴BE=BD=3；（4分）
（2）解：由相交弦定理得AE•BE=GE•FE=6
∴AE=2
（5分）
∵PB切⊙O于点B，AB为⊙O的直径
∴∠ABP=∠ACB=90°
又∵BE=BD=3，
∴∠1=∠2
∵∠1=∠A+∠4，∠2=∠3+∠5
又∵∠5=∠A，
∴∠3=∠4（7分）
方法一：易证△PBD∽△PAE，
∴
=
△PDC∽△PEB
∴
=
（9分）
∴
=
，DC=
=
=
（10分）
在Rt△ACB中，sinA=
=
=
=
=
∴∠A=60°；（12分）
方法二：易证△PBC∽△PAB，
∴
=
∵△PBD∽△PAE
∴
=
（9分）
∴
=
（10分）
sin∠A=
=
=
=
∴∠A=60°（12分）
∴△=（-6）2-4（m2+4m+13）=-4（m+2）2≥0，∴m=-2，（2分）
原方程为x2-6x+9=0，
解之，得x1=x2=3，
∴BE=BD=3；（4分）
（2）解：由相交弦定理得AE•BE=GE•FE=6
| 3 |
∴AE=2
| 3 |
∵PB切⊙O于点B，AB为⊙O的直径
∴∠ABP=∠ACB=90°
又∵BE=BD=3，
∴∠1=∠2
∵∠1=∠A+∠4，∠2=∠3+∠5
又∵∠5=∠A，
∴∠3=∠4（7分）
方法一：易证△PBD∽△PAE，
∴
| BD |
| AE |
| PD |
| PE |
△PDC∽△PEB
∴
| DC |
| EB |
| PD |
| PE |
∴
| BD |
| AE |
| DC |
| EB |
| BD•EB |
| AE |
| 3×3 | ||
2
|
3
| ||
| 2 |
在Rt△ACB中，sinA=
| BC |
| AB |
3+
| ||||
3+2
|
6+3
| ||
6+4
|
3(2+
| ||||
2
|
| ||
| 2 |
∴∠A=60°；（12分）
方法二：易证△PBC∽△PAB，
∴
| BC |
| AB |
| PB |
| PA |
∵△PBD∽△PAE
∴
| BD |
| AE |
| PB |
| PA |
∴
| BC |
| AB |
| BD |
| AE |
sin∠A=
| BC |
| AB |
| BD |
| AE |
| 3 | ||
2
|
| ||
| 2 |
∴∠A=60°（12分）
点评：本题综合考查了学生圆的有关知识，及一元二次方程根的判别式的性质．本题的综合性质很强，所以学生在学习时思维一定要开阔，要把各知识系统起来．
练习册系列答案
相关题目
22、已知，如图AB是⊙O的直径，BC是⊙O的弦，⊙O的割线PDE垂直于AB于点F，交BC于点G，∠A=∠BCP．
（2002•西藏）已知，如图AB是⊙O的直径，半径OC⊥AB，弦CD与AB交于点E．
已知：如图AB是半圆0的直径，点C在半圆上，CD⊥AB，垂足为D，切线PC交BA的延长线于点P，AD，DB的长是关于x的方程x2-（4m+2）+4m2=0（m＞0）的两根，且AD：DB=1：4，求：PO、PC的长．
，求∠A的度数．