题目内容
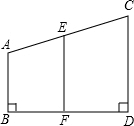 如图,AB⊥BD,CD⊥BD,∠A+∠AEF=180°以下是某同学说明CD∥EF的推理过程或理由,请你在横线上补充完整其推理过程或理由.
如图,AB⊥BD,CD⊥BD,∠A+∠AEF=180°以下是某同学说明CD∥EF的推理过程或理由,请你在横线上补充完整其推理过程或理由.解:因为AB⊥BD,CD⊥BD(已知)
所以∠ABD=∠CDB=90°(垂直定义)
所以∠ABD+∠CDB=180°
所以 AB∥
CD
CD
(同旁内角互补,两直线平行
同旁内角互补,两直线平行
)因为∠A+∠AEF=180°(已知)
所以AB∥EF(
同旁内角互补,两直线平行
同旁内角互补,两直线平行
)所以 CD∥EF(
平行于同一条直线的两直线平行
平行于同一条直线的两直线平行
)分析:根据平行线的判定推出AB∥CD,AB∥EF,即可推出CD∥EF.
解答:解:∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴∠B+∠D=180°,
∴AB∥CD(同旁内角互补,两直线平行),
∵∠A+∠AEF=180°,
∴AB∥EF(同旁内角互补,两直线平行),
∴CD∥EF(平行于同一直线的两直线平行),
故答案为:CD,同旁内角互补,两直线平行,同旁内角互补,两直线平行,平行于同一直线的两直线平行.
∴∠B=∠D=90°,
∴∠B+∠D=180°,
∴AB∥CD(同旁内角互补,两直线平行),
∵∠A+∠AEF=180°,
∴AB∥EF(同旁内角互补,两直线平行),
∴CD∥EF(平行于同一直线的两直线平行),
故答案为:CD,同旁内角互补,两直线平行,同旁内角互补,两直线平行,平行于同一直线的两直线平行.
点评:本题考查了平行线判定的应用,注意:同旁内角互补,两直线平行.

练习册系列答案
相关题目
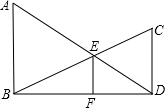 已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明
已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明
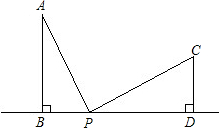 如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在直线BD上,由B点到D点移动,
如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在直线BD上,由B点到D点移动, 如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.
如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED. 如图,AB=BD,BC=BE,∠ABD=∠EBC,则有
如图,AB=BD,BC=BE,∠ABD=∠EBC,则有 如图,AB⊥BD,CD⊥BD,AD=CB.求证:AD∥BC.
如图,AB⊥BD,CD⊥BD,AD=CB.求证:AD∥BC.