题目内容
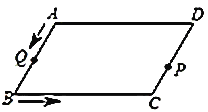
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 与点
与点![]() 是平行四边形
是平行四边形![]() 边上的动点,点
边上的动点,点![]() 以每秒
以每秒![]() 个单位长度的速度,从点
个单位长度的速度,从点![]() 运动到点
运动到点![]() ,点
,点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() →点
→点![]() →点
→点![]() 运动.当其中一个点到达终点时,另一个随之停止运动.点
运动.当其中一个点到达终点时,另一个随之停止运动.点![]() 与点
与点![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)![]() 为何值时,将
为何值时,将![]() 以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
【答案】(1)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;(2)
;(2)![]() 时,
时,![]() 不是等腰三角形,所以不存在符合条件的菱形. 当
不是等腰三角形,所以不存在符合条件的菱形. 当![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
【解析】
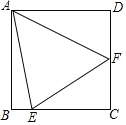
(1)当0<t≤2时,如图1,过点B作BE⊥CD,交DC的延长线于点E,根据三角形面积公式求得S关于t的函数关系式,当2<t≤4时,如图2,CP=t,BQ=2t-4,过点P作PF⊥BC,交BC的延长线于F点,由三角形面积公式求得S关于t的函数关系式,
(2)要使翻折前后的两个三角形所组成的四边形为菱形,则△CPQ为等腰三角形,则要CQ=CP,看看t是否存在.
(1)①当![]() 时,如图1,过点
时,如图1,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,
∴∠BED=90°,即∠BCE+∠CBE=90°,
∵四边形![]() 是平行四边形,∴AD∥BC,
是平行四边形,∴AD∥BC,
![]()
![]() ,
,![]()
![]()
![]() ,由勾股定理得:
,由勾股定理得:![]() ,
,
∵![]() ,
,
∴![]() ;
;
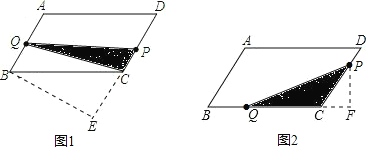
②当![]() 时,由题意得:CP=t,
时,由题意得:CP=t,![]() ,
,![]() ,
,
如图2,过点P作PF⊥BC,交BC的延长线于点F,
∴∠F=90°,
∵四边形![]() 是平行四边形,∴AB∥DC,
是平行四边形,∴AB∥DC,
∴![]() ,∵
,∵![]() ,
,
![]()
![]() ,
,
![]()
![]() ,由勾股定理得:
,由勾股定理得:![]() ,
,
∴![]() ,
,
即![]() .
.
∴S=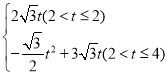 .
.
(2)当![]() 时,
时,![]() 不是等腰三角形,所以不存在符合条件的菱形.
不是等腰三角形,所以不存在符合条件的菱形.
当![]() 时,令
时,令![]() ,即
,即![]() ,解得
,解得![]()
![]() 当
当![]() 时,
时,![]() 为等腰三角形,
为等腰三角形,
即为![]() 的一边所在直线为轴翻折,翻折前后的两个三角形组成的四边形为菱形.
的一边所在直线为轴翻折,翻折前后的两个三角形组成的四边形为菱形.

【题目】随着出行方式的多样化,我市三类打车方式的收费标准如下:
出租车 | 滴滴快车 | 同城快车 |
3千米以内:8元 | 路程:1.4元/千米 | 路程:1.8元/千米 |
超过3千米的部分:2.4元/千米 | 时间:0.6元/分钟 | 时间:0.4元/分钟 |
如:假设打车的平均车速为40千米/小时,乘坐8千米,耗时8÷40×60=12分钟,出租车的收费为:8+2.4×(8﹣3)=20(元);滴滴快车的收费为:8×1.4+12×0.6=18.4(元);同城快车的收费为:8×1.8+12×0.4=19.2(元)
解决问题:
(1)小明乘车从高邮文体公园去盂城驿,全程10千米,如果小明使用滴滴快车,需要支付的打车费用为 元;
(2)小丽乘车从甲地去乙地,用滴滴快车比乘坐出租车节省了28.8元,求甲、乙两地的距离;
(3)同城快车为了和滴滴快车竞争客户,分别推出了优惠方式:滴滴快车对于乘车路程在5千米以上(含5千米)的客户每次收费立减11元;同城快车车费对折优惠.通过计算,对同城快车和滴滴快车两种打车方式,采用哪一种打车方式更合算提出你的建议.