题目内容
两个以点O为圆心的同心圆中，大圆的弦AB与小圆相切，如果AB的长为24，大圆的半径OA为13，那么小圆的半径为________．
5
分析：连接过切点的半径，根据切线的性质定理和垂径定理得半弦是12，再根据勾股定理得小圆的半径是5．
解答：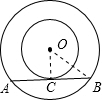
解：∵AB=24，OB=OA=13，
∴BC=12；
在RT△OCB中，
∴OC=
=5．
点评：此题综合运用了切线的性质定理、垂径定理和勾股定理．
分析：连接过切点的半径，根据切线的性质定理和垂径定理得半弦是12，再根据勾股定理得小圆的半径是5．
解答：
解：∵AB=24，OB=OA=13，∴BC=12；
在RT△OCB中，
∴OC=
=5．点评：此题综合运用了切线的性质定理、垂径定理和勾股定理．
练习册系列答案
相关题目
在直角坐标系中，A（0，4），B（4
在Rt△ABC中，∠B=90°，B（0，0），A（0，4），C（4
