题目内容
如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于( )

A.90° B.180° C.210° D.270°
考点:平行线的性质.
分析:根据两直线平行,同旁内角互补求出∠B+∠C=180°,从而得到以点B.点C为顶点的五边形的两个外角的度数之和等于180°,再根据多边形的外角和定理列式计算即可得解.
解答:解:∵AB∥CD,
∴∠B+∠C=180°,
∴∠4+∠5=180°,
根据多边形的外角和定理,∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°﹣180°=180°.
故选B.

点评:本题考查了平行线的性质,多边形的外角和定理,是基础题,理清求解思路是解题的关键.

练习册系列答案
相关题目
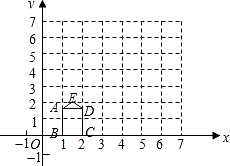 如图,矩形ABCD的长,宽分别为
如图,矩形ABCD的长,宽分别为
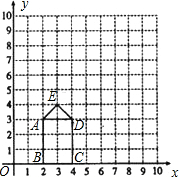 如图,矩形ABCD的长、宽分别为3和2,OB=2,点E的坐标为(3,4)连接AE、ED.
如图,矩形ABCD的长、宽分别为3和2,OB=2,点E的坐标为(3,4)连接AE、ED. 如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见:
如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见: