题目内容
P为Rt△ABC直角边AC上一定点．试在另两边上各求一点Q与R，使△PQR周长最小．
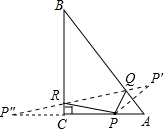解：如图，设P′，P″分别为P关于AB、BC的对称点，P′P″交AB于Q，BC于R．即△PQR为所求．
分析：作点P关于BC的对称点P″，作点P关于BA的对称点P′，连接P′P″交AB于Q，BC于R，由两点之间线段最短可知△PQR周长最小即为所求点．
点评：本题考查的是最短线路问题，根据两点之间线段最短的知识作出P的对称点是解答此题的关键．
练习册系列答案
习题精选系列答案
相关题目
如图，已知等腰Rt△ABC直角边长为1，以它的斜边AC为直角边画第二个等腰Rt△ACD，再以斜边AD为直角边画第三个Rt△ADE…，依此类推，AC长为