题目内容
 如图,在12×7的网格图中(每个小正方形的边长均为1个单位).⊙A的半径为1,⊙B的半径为2,要使⊙A与静止的⊙B外切,那么⊙A位置需向右平移多少个单位
如图,在12×7的网格图中(每个小正方形的边长均为1个单位).⊙A的半径为1,⊙B的半径为2,要使⊙A与静止的⊙B外切,那么⊙A位置需向右平移多少个单位
- A.2
- B.8
- C.2或8
- D.2或4或6或8
C
分析:由⊙A与静止的⊙B外切和由⊙A的半径为1,⊙B的半径为2,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系,即可求得AB的长,继而可求得答案.
解答:∵⊙A的半径为1,⊙B的半径为2,
∴⊙A与静止的⊙B外切时,则AB=2+1=3,
∴当⊙A由图示位置需向右平移2或8时,⊙A与静止的⊙B外切,
故选C.
点评:此题考查了圆与圆的位置关系.此题难度适中,解题的关键是掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.
分析:由⊙A与静止的⊙B外切和由⊙A的半径为1,⊙B的半径为2,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系,即可求得AB的长,继而可求得答案.
解答:∵⊙A的半径为1,⊙B的半径为2,
∴⊙A与静止的⊙B外切时,则AB=2+1=3,
∴当⊙A由图示位置需向右平移2或8时,⊙A与静止的⊙B外切,
故选C.
点评:此题考查了圆与圆的位置关系.此题难度适中,解题的关键是掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
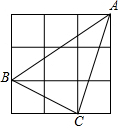 如果小强将飞镖随意的投到如图3×3的正方形网中,那么飞镖落在△ABC中的概率是( )
如果小强将飞镖随意的投到如图3×3的正方形网中,那么飞镖落在△ABC中的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 (2013•南通一模)某花木公司在20天内销售一批马蹄莲.其中,该公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)部分对应值如下表所示.
(2013•南通一模)某花木公司在20天内销售一批马蹄莲.其中,该公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)部分对应值如下表所示.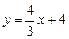 分别交
分别交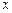 轴,
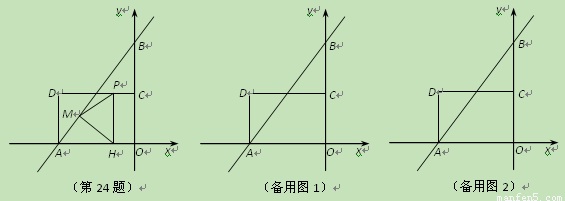
轴,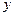 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.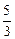 个单位长度的速度向终点B运动,过点P作
个单位长度的速度向终点B运动,过点P作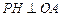 ,垂足为H,连接
,垂足为H,连接 ,
,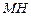 .设点P的运动时间为
.设点P的运动时间为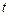 秒.
秒.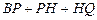 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.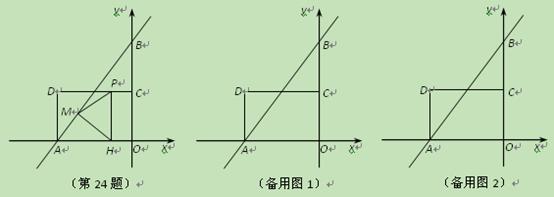
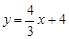 分别交
分别交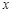 轴,
轴,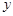 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.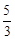 个单位长度的速度向终点B运动,过点P作
个单位长度的速度向终点B运动,过点P作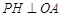 ,垂足为H,连接
,垂足为H,连接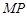 ,
,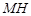 .设点P的运动时间为
.设点P的运动时间为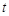 秒.
秒.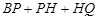 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.