题目内容
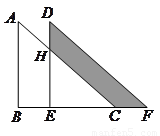
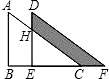 如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF.如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分面积为( )
如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF.如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分面积为( )| A、24cm2 | B、25cm2 | C、26cm2 | D、27cm2 |
分析:根据已知可得到△BAC∽△EHC,从而可得到相似比,根据相似比求得BC的长,从而根据S△ABC-S△EHC求得阴影部分的面积.
解答:解:法1:∵∠B=∠E=90°
∴AB∥EH
∴△BAC∽△EHC
∵AB=8cm,BE=4cm,DH=3cm
∴EH=DE-DH=5cm
∴相似比为
设BC=x,则:
=
∴x=
∴S△ABC=
×
×8=
cm2
=(
)2=
∴S△EHC=
×
=
cm2
∴图中阴影部分面积=
-
=26 cm2;
法2:由平移可得△ABC≌△DEF,
∴S△ABC=S△DEF,
∴S△ABC-S△HEC=S△DEF-S△HEC,即S阴影=S梯形ABEH,
又S梯形ABEH=
BE(HE+AB)=
×4×(8+8-3)=26cm2.
故选C.
∴AB∥EH

∴△BAC∽△EHC
∵AB=8cm,BE=4cm,DH=3cm
∴EH=DE-DH=5cm
∴相似比为
| 5 |
| 8 |
设BC=x,则:
| x-4 |
| x |
| 5 |
| 8 |
∴x=
| 32 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 32 |
| 3 |
| 128 |
| 3 |
| S△ABC |
| S△ECH |
| 5 |
| 8 |
| 25 |
| 68 |
∴S△EHC=
| 25 |
| 64 |
| 128 |
| 3 |
| 50 |
| 3 |
∴图中阴影部分面积=
| 128 |
| 3 |
| 50 |
| 3 |
法2:由平移可得△ABC≌△DEF,
∴S△ABC=S△DEF,
∴S△ABC-S△HEC=S△DEF-S△HEC,即S阴影=S梯形ABEH,
又S梯形ABEH=
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.

练习册系列答案
相关题目
 如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF.如果AB=8cm,BE=4cm,DH=3cm,则图中线段CF为
如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF.如果AB=8cm,BE=4cm,DH=3cm,则图中线段CF为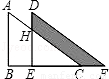
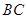 方向平移得到
方向平移得到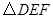 .如果
.如果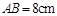 ,
,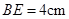 ,
,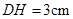 ,则图中阴影部分面积为 cm2.
,则图中阴影部分面积为 cm2.