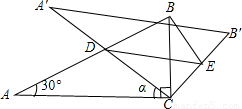
题目内容
如图,将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD,连接CD.若AB=4cm.则△BCD的面积为( )
A.4

B.2

C.3
D.2
【答案】分析:过D点作BE的垂线,垂足为F,由∠ABC=30°及旋转角∠ABE=150°可知∠CBE为平角,在Rt△ABC中,AB=4,∠ABC=30°,则AC=2,BC=2 ,由旋转的性质可知BD=BC=2
,由旋转的性质可知BD=BC=2 ,DE=AC=2,BE=AB=4,由面积法:DF×BE=BD×DE求DF,则S△BCD=
,DE=AC=2,BE=AB=4,由面积法:DF×BE=BD×DE求DF,则S△BCD= ×BC×DF.
×BC×DF.
解答: 解:过D点作BE的垂线,垂足为F,
解:过D点作BE的垂线,垂足为F,
∵∠ABC=30°,∠ABE=150°
∴∠CBE=∠ABC+∠ABE=180°,
∵在Rt△ABC中,AB=4,∠ABC=30°,
∴AC=2,BC=2 ,
,
由旋转的性质可知BD=BC=2 ,DE=AC=2,BE=AB=4,
,DE=AC=2,BE=AB=4,
由DF×BE=BD×DE,即DF×4=2 ×2,
×2,
解得DF= ,
,
S△BCD= ×BC×DF=
×BC×DF= ×2
×2 ×
× =3cm2.
=3cm2.
故答案为:3cm2.
点评:本题考查了旋转的性质,解直角三角形的方法,解答本题的关键是围绕求△BCD的面积确定底和高的值,有一定难度.
 ,由旋转的性质可知BD=BC=2
,由旋转的性质可知BD=BC=2 ,DE=AC=2,BE=AB=4,由面积法:DF×BE=BD×DE求DF,则S△BCD=
,DE=AC=2,BE=AB=4,由面积法:DF×BE=BD×DE求DF,则S△BCD= ×BC×DF.
×BC×DF.解答:
 解:过D点作BE的垂线,垂足为F,
解:过D点作BE的垂线,垂足为F,∵∠ABC=30°,∠ABE=150°
∴∠CBE=∠ABC+∠ABE=180°,
∵在Rt△ABC中,AB=4,∠ABC=30°,
∴AC=2,BC=2
 ,
,由旋转的性质可知BD=BC=2
 ,DE=AC=2,BE=AB=4,
,DE=AC=2,BE=AB=4,由DF×BE=BD×DE,即DF×4=2
 ×2,
×2,解得DF=
 ,
,S△BCD=
 ×BC×DF=
×BC×DF= ×2
×2 ×
× =3cm2.
=3cm2.故答案为:3cm2.
点评:本题考查了旋转的性质,解直角三角形的方法,解答本题的关键是围绕求△BCD的面积确定底和高的值,有一定难度.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 C,△ABC的面积为S△ABC.
C,△ABC的面积为S△ABC. 交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.
交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.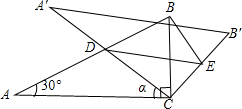 交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.
交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.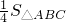 时,判断⊙E与A′C的位置关系,并求相应的tanα值.
时,判断⊙E与A′C的位置关系,并求相应的tanα值.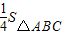 时,判断⊙E与A′C的位置关系,并求相应的tanα值.
时,判断⊙E与A′C的位置关系,并求相应的tanα值.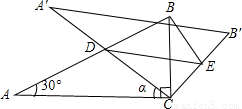
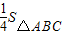 时,判断⊙E与A′C的位置关系,并求相应的tanα值.
时,判断⊙E与A′C的位置关系,并求相应的tanα值.