题目内容
(1)
(2)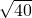 -5
-5 +
+
(3)求满足条件的x的值:64(x-1)2=49
(4)已知实数a、b满足(a-2)2+ =0,求b-a的平方根.
=0,求b-a的平方根.
解:(1)原式= =
= =5;
=5;
(2)原式=2 -
- +
+ =
= ;
;
(3)(x-1)2= ,
,
x-1=± ,
,
所以x1= ,x2=
,x2= ;
;
(4)根据题意得a-2=0,b-2a=0,
解得a=2,b=4,
b-a=4-2=2,
所以b-a的平方根为± .
.
分析:(1)先把分子的各二次根式化为最简二次根式,然后合并后进行二次根式的除法运算;
(2)先把各二次根式化为最简二次根式,然后合并;
(3)先变形得到(x-1)2= ,再根据平方根的定义得x-1=±
,再根据平方根的定义得x-1=± ,然后解一次方程即可;
,然后解一次方程即可;
(4)根据非负数的性质得到a-2=0,b-2a=0,解得a=2,b=4,然后根据平方根的定义计算b-a的平方根.
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,在进行二次根式的乘除运算,然后合并同类二次根式.也考查了平方根和非负数的性质.
 =
= =5;
=5;(2)原式=2
 -
- +
+ =
= ;
;(3)(x-1)2=
 ,
,x-1=±
 ,
,所以x1=
 ,x2=
,x2= ;
;(4)根据题意得a-2=0,b-2a=0,
解得a=2,b=4,
b-a=4-2=2,
所以b-a的平方根为±
 .
.分析:(1)先把分子的各二次根式化为最简二次根式,然后合并后进行二次根式的除法运算;
(2)先把各二次根式化为最简二次根式,然后合并;
(3)先变形得到(x-1)2=
 ,再根据平方根的定义得x-1=±
,再根据平方根的定义得x-1=± ,然后解一次方程即可;
,然后解一次方程即可;(4)根据非负数的性质得到a-2=0,b-2a=0,解得a=2,b=4,然后根据平方根的定义计算b-a的平方根.
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,在进行二次根式的乘除运算,然后合并同类二次根式.也考查了平方根和非负数的性质.

练习册系列答案
相关题目
 如图,
如图, 路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子
路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子 如图,△ABC中BD、CD平分∠ABC、∠ACB,过D作直线平行于BC,交AB、AC于E、F,AB=5,AC=7,BC=8,△AEF的周长为
如图,△ABC中BD、CD平分∠ABC、∠ACB,过D作直线平行于BC,交AB、AC于E、F,AB=5,AC=7,BC=8,△AEF的周长为 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a、b,那么(a-b)2的值是
我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a、b,那么(a-b)2的值是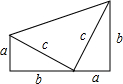 在一张纸上画两个全等的直角三角形,并把它们拼成如图形状,请用两种方法表示这个梯形的面积.利用你的表示方法,你能得到勾股定理吗?
在一张纸上画两个全等的直角三角形,并把它们拼成如图形状,请用两种方法表示这个梯形的面积.利用你的表示方法,你能得到勾股定理吗?