题目内容
如图：D为BC中点，E为AD中点，则△BED面积与△ACD面积之比为________．
1：2
分析：根据中线的定义得到DB=CD，AE=DE，然后根据等底等高的三角形的面积相等即可求解．
解答：∵D为BC中点，
∴DB=CD，
∴S△ABD=S△ACD，
∵E为AD中点，
∴AE=DE，
∴S△ABE=S△BDE=
S△ABD=S△ACD，
∴△BED面积与△ACD面积之比为1：2．
故答案为：1：2．
点评：本题考查了三角形面积：三角形的面积等于底边与底边上的高的积一半；等底等高的三角形的面积相等．
分析：根据中线的定义得到DB=CD，AE=DE，然后根据等底等高的三角形的面积相等即可求解．
解答：∵D为BC中点，
∴DB=CD，
∴S△ABD=S△ACD，
∵E为AD中点，
∴AE=DE，
∴S△ABE=S△BDE=
S△ABD=S△ACD，∴△BED面积与△ACD面积之比为1：2．
故答案为：1：2．
点评：本题考查了三角形面积：三角形的面积等于底边与底边上的高的积一半；等底等高的三角形的面积相等．
练习册系列答案
相关题目
如图：D为BC中点，E为AD中点，则△BED面积与△ACD面积之比为
APCD，AC与PD相交于点E，已知∠ABC=∠AEP=
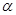(0°<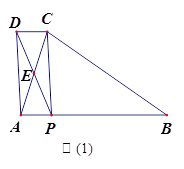
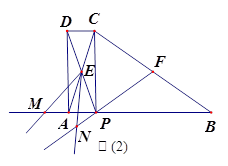
APCD，AC与PD相交于点E，已知∠ABC=∠AEP=
(0°<
APCD是否为矩形?请说明理由;
