题目内容
一次同学聚会中,见面时两两握手一次,共握手28次.则这次参加聚会的有( )人.
- A.9
- B.7
- C.4
- D.8
D
分析:等量关系为:人数×(人数-1)÷2=握手的总次数,把相关数值代入即可求解.
解答:设这次参加聚会的有x人,每个人都要与(x-1)个人握手一次,但两人只握手一次.则:
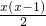 =28,
=28,
解得x1=8,x2=-7,
∵人数不为负数,
∴x=8,故选D.
点评:解决本题的关键是找到握手总次数的等量关系;注意每个人都要与除自己外的其他人握手一次,但两人只握手一次.
分析:等量关系为:人数×(人数-1)÷2=握手的总次数,把相关数值代入即可求解.
解答:设这次参加聚会的有x人,每个人都要与(x-1)个人握手一次,但两人只握手一次.则:
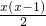 =28,
=28,解得x1=8,x2=-7,
∵人数不为负数,
∴x=8,故选D.
点评:解决本题的关键是找到握手总次数的等量关系;注意每个人都要与除自己外的其他人握手一次,但两人只握手一次.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一次同学聚会中,见面时两两握手一次,共握手28次.则这次参加聚会的有( )人.
| A、9 | B、7 | C、4 | D、8 |