Question

【题目】若抛物线与x轴的两个交点及其顶点构成等边三角形，则称该抛物线“等边抛物线”.

(1)若对任意m，n，点M(m，n)和点N（-m+4，n）恒在“等边抛物线”：上，求抛物线的解析式；

(2)若抛物线：“等边抛物线”，求的值；

(3)对于“等边抛物线”：，当1<x<m吋，总存在实数b。使二次函数的图象在一次函数y=x图象的下方，求m的最大值.

Answer 1

【答案】（1）或；（2）；（3）m的最大值为6.

【解析】

（1）先由点M和点N关于对称轴对称，可得对称轴x=2，依据x=，可得b=-4a，从而得，然后分a＞0和a＜0两种情况讨论，根据等边三角形性质得出顶点坐标，代入计算即可；

（2）设等边抛物线与x轴的两个交点分别为，，知，结合顶点坐标，可得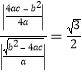：，由此即可求出；

（3）由（2）中可得，结合该等边抛物线过（1，1），求得b=-6或b=2，依据对称轴位置可知b=-6，联立，解得x=1或x=6，从而得出答案.

解：（1）由题意得，点M和点N关于对称轴对称，

∴对称轴x=，

∴x=，

∴b=-4a，

∴，

①当a＞0时，顶点坐标为（2，-2），

代入，得-2=4a-8a，

解得：a=，

∴；

②当a＜0时，顶点坐标为（2，2），

代入，得2=4a-8a，

解得：a=，

∴；

综上，或；

（2）设等边抛物线与x轴的两个交点分别为，，

令，∴，

∴，

又∵抛物线顶点坐标为，

∴，∵，

∴，

∴

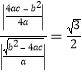（3）由（2）得，∴，

∴：，

由题意可得该等边抛物线过（1，1），

∴，

解得：b=-6或b=2，

又对称轴x=，

∴b＜-2，

∴b=-6，

∴，

联立，

解得x=1或x=6，

∴m的最大值为6.