题目内容
 如图,已知四边形ABCD内接于直径为3的圆O,对角线AC是直径,对角线AC和BD的交点是P,AB=BD,且PC=0.6,求四边形ABCD的周长.
如图,已知四边形ABCD内接于直径为3的圆O,对角线AC是直径,对角线AC和BD的交点是P,AB=BD,且PC=0.6,求四边形ABCD的周长.
 解:设圆心为O,连接BO并延长交AD于H.
解:设圆心为O,连接BO并延长交AD于H.∵△ABD是⊙O的内接三角形,AB=BD,
∴OB平分∠ABD,
∵AB=BD,O是圆心,
∴BH⊥AD.
又∵∠ADC=90°,
∴BH∥CD,
 =
= ,
,即:
 =
= ,
,∴CD=1.
于是AD=
 =
= =2
=2 .
.又OH=
 CD=
CD= ,于是
,于是AB=
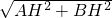 =
= =
= .
.BC=
 =
= =
= .
.所以,四边形ABCD的周长为:1+2
 +
+ +
+ .
.分析:连接BO并延长,得到BH⊥AD,可以证明两三角形相似,利用相似三角形的性质求出CD的长,然后运用勾股定理求出AD,AB和BC的长,再计算出四边形的周长.
点评:本题考查的是相似三角形的判定与性质,根据垂径定理可以得到BH⊥AD,然后用两直线平行判定两三角形相似,利用相似三角形的性质计算求出CD的长,再在直角三角形中用勾股定理计算求出四边形另外三边的长,得到四边形ABCD的周长.

练习册系列答案
相关题目
 15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且 (2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
(2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
