��Ŀ����
���ڡ�C���C�ϵ�һ��A����ƽ���ڵĵ�P���㣺����AP���C���ڵ�Q����Q�������P�غϣ�����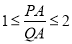 �����P��Ϊ��A���ڡ�C�ġ������㡱��
�����P��Ϊ��A���ڡ�C�ġ������㡱��
��֪��OΪ����ԭ�㣬��O�İ뾶Ϊ1����A��-1��0����
��1������P�ǵ�A���ڡ�O�ġ������㡱���ҵ�P��x���ϣ���д��һ�����������ĵ�P������________��
��2������B�ǵ�A���ڡ�O�ġ������㡱��������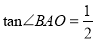 �����B��������t��ȡֵ��Χ��
�����B��������t��ȡֵ��Χ��
��3��ֱ��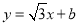 ��x�ύ�ڵ�M����y�ύ�ڵ�N�����߶�MN�ϴ��ڵ�A���ڡ�O�ġ������㡱��ֱ��д��b��ȡֵ��Χ��_____________________________��
��x�ύ�ڵ�M����y�ύ�ڵ�N�����߶�MN�ϴ��ڵ�A���ڡ�O�ġ������㡱��ֱ��д��b��ȡֵ��Χ��_____________________________��
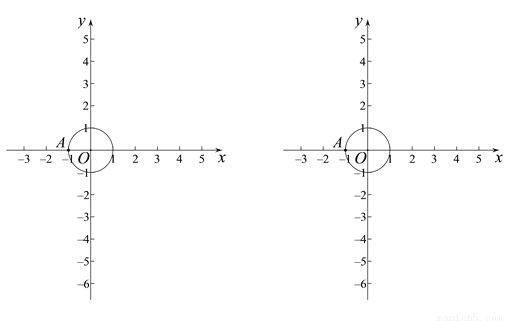
��ϰ��ϵ�д�
�����Ŀ


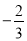 �Ҵ���Ϊ3�ĵ���ʽ __________��
�Ҵ���Ϊ3�ĵ���ʽ __________��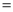 90�㣬AB
90�㣬AB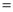 AC��
AC��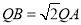 ���Ƿ���ȷ��________����ǡ�����
���Ƿ���ȷ��________����ǡ�����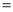
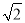 PA��
PA��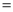 30�㣬���PAB�Ĵ�С��
30�㣬���PAB�Ĵ�С��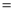 ������BPC
������BPC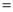 �£��õ�ʽ��ʾ������֮���������ϵ����֤����Ľ��ۣ�
�£��õ�ʽ��ʾ������֮���������ϵ����֤����Ľ��ۣ�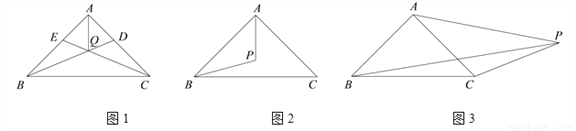
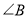 �Ĵ�СΪ��������
�Ĵ�СΪ��������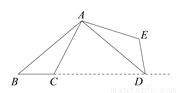
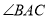 Ϊ��ǣ�ͼ2��
Ϊ��ǣ�ͼ2��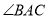 Ϊֱ�ǣ�ͼ3��
Ϊֱ�ǣ�ͼ3��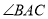 Ϊ�۽ǣ���
Ϊ�۽ǣ���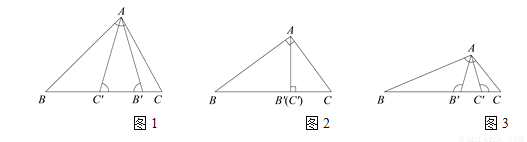
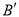 ��
�� 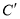 ���㣬ʹ
���㣬ʹ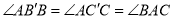 ����
����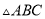 ��
��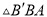 ��
��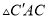 ��
�� 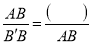 ��
�� 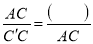 �������ɵ�
�������ɵ�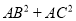
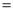 ������
������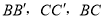 ��ʾ��
��ʾ��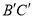
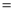 ��
��