题目内容
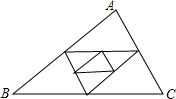
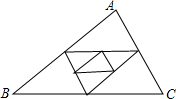
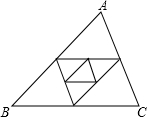 已知△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2010个三角形的周长为
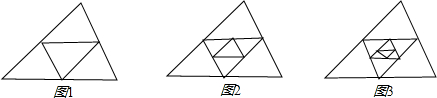
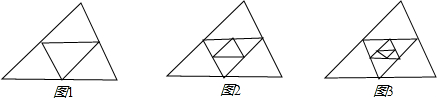
已知△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2010个三角形的周长为分析:根据已知条件,首先可知各三角形都相似,然后根据题意可得规律:第n个三角形与原三角形的相似比为1:2n-1,又由△ABC周长为1,即可求得第2010个三角形的周长.
解答:解:∵连接△ABC三边中点构成第二个三角形,
∴新三角形的三边与原三角形的三边的比值为1:2,
∴它们相似,且相似比为1:2,
同理:第三个三角形与第二个三角形的相似比为1:2,
即第三个三角形与第一个三角形的相似比为:1:22,
以此类推:第2010个三角形与原三角形的相似比为1:22009,
∵△ABC周长为1,
∴第2010个三角形的周长为
.
故答案为:
.
∴新三角形的三边与原三角形的三边的比值为1:2,
∴它们相似,且相似比为1:2,
同理:第三个三角形与第二个三角形的相似比为1:2,
即第三个三角形与第一个三角形的相似比为:1:22,
以此类推:第2010个三角形与原三角形的相似比为1:22009,
∵△ABC周长为1,
∴第2010个三角形的周长为
| 1 |
| 22009 |
故答案为:
| 1 |
| 22009 |
点评:此题考查了相似三角形的性质与三角形中位线的性质.此题难度较大,解题的关键是找到规律:第n个三角形与原三角形的相似比为1:2n-1.

练习册系列答案
相关题目
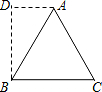 如图,在等边三角形ABC中,BD⊥BC,过A作AD⊥BD于D,已知△ABC周长为M,则AD=( )
如图,在等边三角形ABC中,BD⊥BC,过A作AD⊥BD于D,已知△ABC周长为M,则AD=( )A、
| ||
B、
| ||
C、
| ||
D、
|
 已知△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2006个三角形的周长为
已知△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2006个三角形的周长为