Question

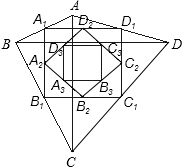如图，已知四边形ABCD的对角线AC=BD，AC⊥BD，四边形A₁B₁C₁D₁的四个顶点A₁、B₁、C₁、D₁分别为AB、BC、CD、DA的中点，四边形A₂B₂C₂D₂的四个顶点A₂、B₂、C₂、D₂分别为A₁B₁、B₁C₁、C₁D₁、D₁A₁的中点，如果AC=2a，那么S_{四边形AnBnCnDn}=________．

Answer 1

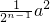
分析：根据三角形的面积公式，可以求得四边形ABCD的面积是2a²；根据三角形的中位线定理，得A₁B₁∥AC，A₁B₁=AC，则△BA₁B₁∽△BAC，得△BA₁B₁和△BAC的面积比是相似比的平方，即，因此四边形A₁B₁C₁D₁的面积是四边形ABCD的面积的，即a²；推而广之，则S_{四边形AnBnCnDn}=．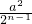
解答：∵四边形A₁B₁C₁D₁的四个顶点A₁、B₁、C₁、D₁分别为AB、BC、CD、DA的中点，
∴A₁B₁∥AC，A₁B₁=AC．
∴△BA₁B₁∽△BAC．
∴△BA₁B₁和△BAC的面积比是相似比的平方，即．
又四边形ABCD的对角线AC=BD=2a，AC⊥BD，
∴四边形ABCD的面积是2a²．
推而广之，则S_{四边形AnBnCnDn}=．
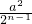点评：此题综合运用了三角形的中位线定理、相似三角形的判定及性质．
注意：对角线互相垂直的四边形的面积等于对角线乘积的一半．