题目内容
【题目】如图9，抛物线y＝ax2＋c（a＞0）经过梯形ABCD的四个顶点，梯形的底AD在x轴上，其中A（－2,0），B（－1, －3）．
（1）求抛物线的解析式；（3分）
（2）点M为y轴上任意一点，当点M到A、B两点的距离之和为最小时，求此时点M的坐标；（2分）
（3）在第（2）问的结论下，抛物线上的点P使S△PAD＝4S△ABM成立，求点P坐标．（4分）
【答案】
（1）
（2）
（3）
【解析】（1）、因为点A、B均在抛物线上，故点A、B的坐标适合抛物线方程
∴
解之得：
；故为所求
（2）如图2，连接BD，交y轴于点M，则点M就是所求作的点
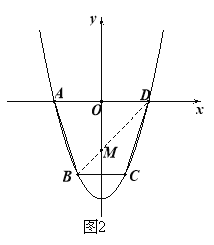
设BD的解析式为
，则有
，
，
故BD的解析式为
；令
则
，故
(3)、如图3，连接AM，BC交y轴于点N，由（2）知，OM=OA=OD=2，
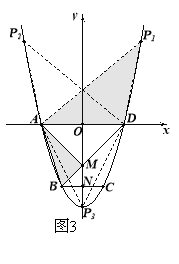
易知BN=MN=1，易求
；设
，
依题意有：
，即：
解之得：
，
，故 符合条件的P点有三个：
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
