题目内容
已知有两张全等的矩形纸片。
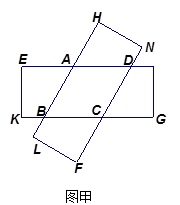
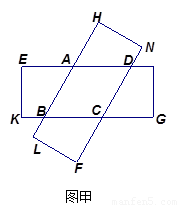
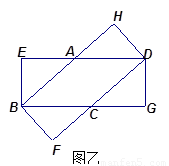
(1)将两张纸片叠合成如图甲,请判断四边形 的形状,并说明理由;
的形状,并说明理由;
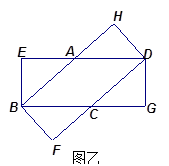
(2)设矩形的长是6,宽是3.当这两张纸片叠合成如图乙时,菱形的面积最大,求此时菱形 的面积.
的面积.
【答案】
解(1)四边形 是菱形。
是菱形。
理由:作AP⊥BC于P,AQ⊥CD于Q
由题意知:AD∥BC,AB∥CD
∴四边形ABCD是平行四边形
∵两个矩形全等
∴AP=AQ
∵AP·BC=AQ·CD ∴BC=CD
∴平行四边形ABCD是菱形

(2)设BC=x,则CG=6-x ,CD=BC=x
在Rt△CDG中,
∴  解得 x=
解得 x=
∴ S=BC·DG=
【解析】(1)作AP⊥BC于P,AQ⊥CD于Q,根据题意先证出四边形ABCD是平行四边形,再由AP=AQ得平行四边形ABCD是菱形;
(2)设BC=x,则CG=6-x,CD=BC=x,在Rt△CDG中,由勾股定理得出x,再求得面积.

练习册系列答案
相关题目
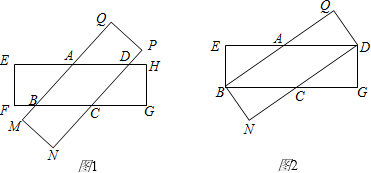 已知有两张全等的矩形纸片.
已知有两张全等的矩形纸片. 的形状,并说明理由;
的形状,并说明理由;