题目内容
在直角△ABC中，∠C=90°．如果以此直角三角形三边为边，分别作三个正三角形（如图），那么面积S1，S2，S3之间有什么关系？
解：在直角△ABC中，∠C=90°，
∴AB2=AC2+BC2，
根据正三角形面积计算S3=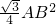
，
S1=
，S2=
，
∴S1+S2=
（BC2+AC2）=AB2=S3，
故S1+S2=S3．
答：S1，S2，S3之间关系为S1+S2=S3．
分析：分别用直角三角形的三边AB，AC，BC表示S1、S2、S3的大小，并且比较S1、S2、S3得出结论．
点评：本题考查了勾股定理的灵活运用，本题中正确的用AC表示S2，BC表示S1，AB表示S3是解题的关键．
∴AB2=AC2+BC2，
根据正三角形面积计算S3=
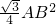，S1=
，S2=，∴S1+S2=
（BC2+AC2）=AB2=S3，故S1+S2=S3．
答：S1，S2，S3之间关系为S1+S2=S3．
分析：分别用直角三角形的三边AB，AC，BC表示S1、S2、S3的大小，并且比较S1、S2、S3得出结论．
点评：本题考查了勾股定理的灵活运用，本题中正确的用AC表示S2，BC表示S1，AB表示S3是解题的关键．
练习册系列答案
相关题目
如图，在直角△ABC中，∠C=90°，BD平分∠ABC且交AC于D，若AP平分∠BAC交BD于P，求∠APB的度数．
已知：如图，在直角△ABC中，AD=DE=EB，且CD2+CE2=1，则斜边AB的长为
如图，在直角△ABC中，∠C=90°，若AB=5，AC=4，则tan∠B=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，在直角△ABC中，∠C=90°，AB的垂直平分线交AB于D，交AC于F，且BE平分∠ABC，则∠A=（ ）
如图，在直角△ABC中，∠A=90°，BC边上的垂直平分线交AC于点D；BD平分∠ABC，已知AC=m+2n，BC=2m+2n，则△BDE的周长为