题目内容
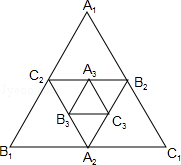
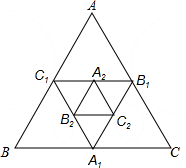如图，小红作出了面积为1的正△ABC，然后分别取△ABC三边的中点A1，B1，C1，作出了正△A1B1C1，用同样的方法，作出了正△A2B2C2，…，由此可得，正△A8B8C8的面积是________．
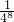
分析：首先由别取△ABC三边的中点A1，B1，C1，根据三角形中位线的性质，可得△A1B1C1∽△ABC，然后由相似三角形面积比等于相似比的平方，即可求得S△A1B1C1=
S△ABC=，继而可得规律：S△AnBnCn=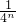
，则可求得答案．解答：∵△ABC三边的中点A1，B1，C1，
∴B1C1=
BC，A1B1=AB，A1C1=AC，∴△A1B1C1∽△ABC，
∴S△A1B1C1=
S△ABC=，同理：S△A2B2C2=
S△A1B1C1=
，∴S△AnBnCn=
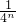，∴正△A8B8C8的面积是：
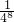．点评：此题考查了相似三角形的判定与性质与三角形中位线的性质．此题难度适中，注意得到规律：S△AnBnCn=
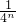是解此题的关键． 
练习册系列答案
相关题目
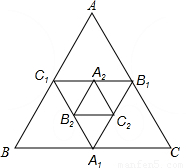
（2011•黔西南州）如图，小红作出了边长为1的第1个正三角形△A1B1C1，算出了正△A1B1C1的面积，然后分别取△A1B1C1三边的中点A2B2C2，作出了第二个正三角形△A2B2C2，算出第2个正△A2B2C2的面积，用同样的方法作出了第3个正△A3B3C3，算出第3个正△A3B3C3的面积，依此方法作下去，由此可得第n次作出的正△AnBnCn的面积是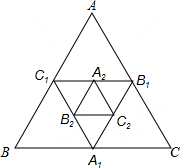
如图，小红作出了面积为1的正△ABC，然后分别取△ABC三边的中点A1，B1，C1，作出了正△A1B1C1，用同样的方法，作出了正△A2B2C2，…，由此可得，正△A8B8C8的面积是
