题目内容
(本题满分7分)
如图6，在△ABC中，∠C=90°，AC+BC=8，∠ACB的平分线交AB于点D，以D为圆心的⊙O与AC相切于点D．
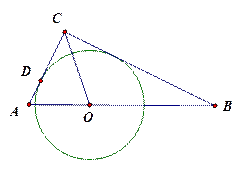
(1)求证: ⊙0与BC相切；
(2)当AC=2时，求⊙O的半径，
如图6，在△ABC中，∠C=90°，AC+BC=8，∠ACB的平分线交AB于点D，以D为圆心的⊙O与AC相切于点D．
(1)求证: ⊙0与BC相切；
(2)当AC=2时，求⊙O的半径，
（1）证明略
（2）
(1)证明略；
(2)解：由(1)知BC与00相切，设BC与00切于点E，连接OD.OE，
∵ D、E为切点，
∴OD⊥AC,OE⊥BC,OD=OE,
S
ABC=SAOC+ SBOC =
∴
AC·BC= AC·OD+BC·OE
∵AC+BC="8" , AC=2,∴BC=6,
∴×2×6=×2×OD+×6×OE,
而OD=OE．
∴OD=，即⊙O的半径为
(2)解：由(1)知BC与00相切，设BC与00切于点E，连接OD.OE，
∵ D、E为切点，
∴OD⊥AC,OE⊥BC,OD=OE,
S
ABC=SAOC+ SBOC =∴
AC·BC= AC·OD+BC·OE ∵AC+BC="8" , AC=2,∴BC=6,
∴
×2×6=×2×OD+×6×OE,而OD=OE．
∴OD=
，即⊙O的半径为
练习册系列答案
相关题目
和半圆
，其中
，证明：
；
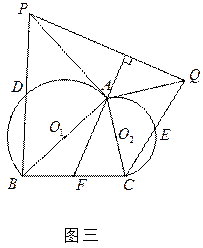
、(0，2)，P是△AOB外接圆上的一点，且∠AOP=45°，则点P的坐标为 ▲ ．
中，
，
是
边上一点，以
为直径的
与边
相切于点
，连结
并延长，与
的延长线交于点
．
；
，求
的直径，弦CD⊥AB于点E，且CD=3cm，⊙O的半径为
cm，则∠CDB的度数为（ ）
的代数式表示）
是
的直径，
为
，则
的度数为__________.
是
的外接圆，
，过点
作
，交
的延长线于点
．
是
，求线段