题目内容
如图,在平面直角坐标系中,抛物线y=ax2+bx-2与x轴交于点A(-1,0)、B(4,0).点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.
(1)求这条抛物线所对应的函数关系式.
(2)求点C在这条抛物线上时m的值.
(3)将线段CN绕点N逆时针旋转90°后,得到对应线段DN.
①当点D在这条抛物线的对称轴上时,求点D的坐标.
②以DN为直角边作等腰直角三角形DNE,当点E在这条抛物线的对称轴上时,直接写出所有符合条件的m值.
(参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(-
,
))

(1)求这条抛物线所对应的函数关系式.
(2)求点C在这条抛物线上时m的值.
(3)将线段CN绕点N逆时针旋转90°后,得到对应线段DN.
①当点D在这条抛物线的对称轴上时,求点D的坐标.
②以DN为直角边作等腰直角三角形DNE,当点E在这条抛物线的对称轴上时,直接写出所有符合条件的m值.
(参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(-
| b |
| 2a |
| 4ac-b2 |
| 4a |

(1)∵抛物线经过点A(-1,0)、B(4,0),
∴
解得
∴抛物线所对应的函数关系式为y=
x2-
x-2;
(2)∵△CMN是等腰直角三角形CMN,∠CMN=90°,
∴CM=MN=2,
∴点C的坐标为(m,2),
∵点C(m,2)在抛物线上,
∴
m2-
m-2=2,
解得m1=
,m2=
.
∴点C在这条抛物线上时,m的值为
或
;
(3)①∵将线段CN绕点N逆时针旋转90°后,得到对应线段DN,
∴∠CND=90°,DN=CN=
CM=
MN,
∴CD=
CN=2CM=2MN,
∴DM=CM=MN,∠DMN=90°,
∴点D的坐标为(m,-2).
又∵抛物线y=
x2-
x-2的对称轴为直线x=
,点D在这条抛物线的对称轴上,
∴点D的坐标为(
,-2);
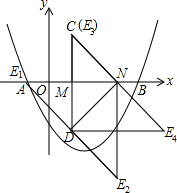 ②如图,以DN为直角边作等腰直角三角形DNE,E点的位置有四种情况:
②如图,以DN为直角边作等腰直角三角形DNE,E点的位置有四种情况:
如果E点在E1的位置时,
∵点D的坐标为(m,-2),MN=ME1=2,点N的坐标为(m+2,0),
∴点E1的(m-2,0),
∵点E1在抛物线y=
x2-
x-2的对称轴直线x=
上,
∴m-2=
,解得m=
;
如果E点在E2的位置时,
∵点D的坐标为(m,-2),点N的坐标为(m+2,0),
∴点E2的(m+2,-4),
∵点E2在抛物线y=
x2-
x-2的对称轴直线x=
上,
∴m+2=
,解得m=-
;
如果E点在E3的位置时,
∵点D的坐标为(m,-2),
∴点E3的(m,2),
∵点E3在抛物线y=
x2-
x-2的对称轴直线x=
上,
∴m=
;
如果E点在E4的位置时,
∵点D的坐标为(m,-2),点N的坐标为(m+2,0),
∴点E4的(m+4,-2),
∵点E4在抛物线y=
x2-
x-2的对称轴直线x=
上,
∴m+4=
,解得m=-
;
综上可知,当点E在这条抛物线的对称轴上时,所有符合条件的m的值为m=-
或m=-
或m=
或m=
.
∴
|
解得
|
∴抛物线所对应的函数关系式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)∵△CMN是等腰直角三角形CMN,∠CMN=90°,
∴CM=MN=2,
∴点C的坐标为(m,2),
∵点C(m,2)在抛物线上,
∴
| 1 |
| 2 |
| 3 |
| 2 |
解得m1=
3+
| ||
| 2 |
3-
| ||
| 2 |
∴点C在这条抛物线上时,m的值为
3+
| ||
| 2 |
3-
| ||
| 2 |
(3)①∵将线段CN绕点N逆时针旋转90°后,得到对应线段DN,
∴∠CND=90°,DN=CN=
| 2 |
| 2 |
∴CD=
| 2 |
∴DM=CM=MN,∠DMN=90°,
∴点D的坐标为(m,-2).
又∵抛物线y=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴点D的坐标为(
| 3 |
| 2 |
 ②如图,以DN为直角边作等腰直角三角形DNE,E点的位置有四种情况:
②如图,以DN为直角边作等腰直角三角形DNE,E点的位置有四种情况:如果E点在E1的位置时,
∵点D的坐标为(m,-2),MN=ME1=2,点N的坐标为(m+2,0),
∴点E1的(m-2,0),
∵点E1在抛物线y=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴m-2=
| 3 |
| 2 |
| 7 |
| 2 |
如果E点在E2的位置时,
∵点D的坐标为(m,-2),点N的坐标为(m+2,0),
∴点E2的(m+2,-4),
∵点E2在抛物线y=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴m+2=
| 3 |
| 2 |
| 1 |
| 2 |
如果E点在E3的位置时,
∵点D的坐标为(m,-2),
∴点E3的(m,2),
∵点E3在抛物线y=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴m=
| 3 |
| 2 |
如果E点在E4的位置时,
∵点D的坐标为(m,-2),点N的坐标为(m+2,0),
∴点E4的(m+4,-2),
∵点E4在抛物线y=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴m+4=
| 3 |
| 2 |
| 5 |
| 2 |
综上可知,当点E在这条抛物线的对称轴上时,所有符合条件的m的值为m=-
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 7 |
| 2 |

练习册系列答案
相关题目


 什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标.
什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标.
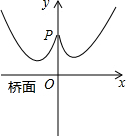 标系,左边的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称.
标系,左边的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称.